In third grade math, Common Core students work on multi‐digit subtraction. The goal is to be able to solve problems such as 753 – 168 quickly, accurately, and with meaning.
Students use a variety of strategies to work these problems. Some students may have a favorite way of thinking about subtraction that they use for all problems; other students may change their strategies depending on the problem.
Here are two examples. Find this difference: 1,002 – 998. Then find this difference: 132 – 76.
Many people solve these two problems in very different ways. Maybe you did too. A common way to solve 1,002 – 998 is to think, "How far apart are 1,002 and 998? Well, 1,000 is between them. 998 is two less than 1,000 and 1,002 is two more than 1,000. So 1,002 – 998 = 4." If you look at the difference as asking how far apart, then you can probably do this problem in your head.
The second problem, 132 – 76, is harder for most people to do in their heads. Not impossible, but harder (for example, 100 is between them — 76 is 24 less, while 132 is 32 more, so 132 and 76 are 56 units apart).
The second problem is one that many people will get out paper and pencil in order to solve. The figure shows the standard algorithm on the left and a different kind of work on the right.
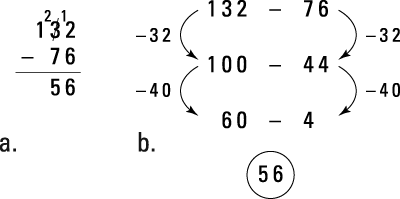
The thinking behind the work on the right is this: You want to take 76 things from a collection of 132 things, so stick to these steps:
Take away 32.
Doing so gets you to a nice, round 100.
Take away another 44 things to total 76 things taken away.
That means the first line (132 – 76) is equal to the second line (100 – 44).
Take the 44 away in two pieces.
First 40 and then 4 more.
To be clear, the work on the right is not the Common Core way of solving this subtraction problem. It is a way of keeping track of a useful thought process — one that involves decomposing numbers (decomposing basically means taking apart without changing the value).
The use of 100 in this computation is an example of using place value. One hundred is a special and important number in the number system; it's the smallest three‐digit number, for example, and it's made of ten tens (and ten is the basis on which the whole number system is built).
You could do the first problem (1002 – 998) using the standard algorithm, and you could do it using the idea of taking away in several steps, as on the right in the figure. However, these methods are a hassle because neither one is easy to do in your head, and there are many opportunities for errors.
Insisting that students have or use only one strategy for solving multi‐digit subtraction problems pretty much guarantees an increased number of computational errors. Put more simply, kids get things wrong more often when they only have one strategy.

