Viewed on their own, the seventh grade standards about angles and triangles can seem a little odd. However, when you see these standards in context, you'll understand why seventh graders study what they do in Common Core math.
The road from elementary school geometry to high school geometry has been rocky. Traditionally, children have spent a great deal of time recognizing and identifying shapes in the primary grades but have encountered a huge gap and advance little in their geometry knowledge until tenth grade, when they're expected to prove geometry theorems.
The Common Core standards seek to fill that gap by slowly making the geometry more challenging at every grade, which means for seventh graders that they're taking on a small part of what is traditionally in a high school geometry course. Seventh graders play around with drawing triangles in an attempt to determine precisely what conditions are necessary in order to know that two triangles are identical to each other (the math term for identical is congruent).
If the triangles have three pairs of congruent sides and three pairs of congruent angles, then the two triangles are congruent, as shown in the figure.
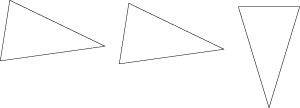
But the three angles of a triangle add up to 180 degrees, so if you only know that two of the three pairs of angles are congruent, the third pair must be, which means that you only need three pairs of sides and two pairs of angles. Seventh graders build this kind of argument as they investigate which conditions must give congruent triangles and which may not.
Studying the properties of angles supports some of this work. A bunch of vocabulary goes along with it. Two angles are supplementary if their measures add to 180 degrees. Two angles are complementary if their measures add to 90 degrees. Two angles are vertical if they result from two intersecting lines but have only a vertex in common. Two angles are adjacent if they share a side.
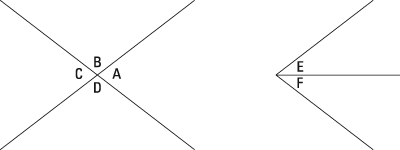
In this figure, angles A and B are supplementary. Angles E and F are complementary. Angles A and C are vertical. Angles A and B are adjacent (and so are E and F).

