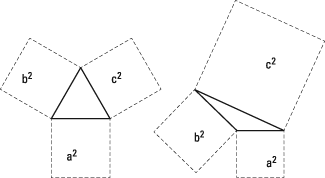
Eighth grade is when students learn the Pythagorean theorem in the Common Core State Standards. The Pythagorean theorem is this: In a right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse.
This definition seems a little bewildering, but the idea isn't nearly so complicated. This figure is simpler to interpret.
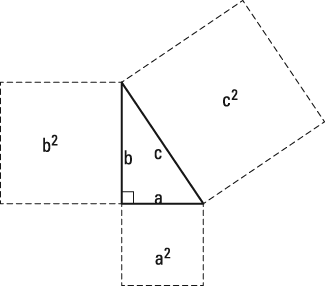
The area of each smaller square is equal to the square of the length of a leg, where a leg is one of the two shorter sides of the right triangle. The area of the largest square is equal to the square of the length of the hypotenuse, where the hypotenuse is the length of the longest side of a right triangle. The Pythagorean theorem says that the areas of the two smaller squares add up to be the same as the area of the largest square.
In symbols, this relationship is stated even more compactly. If a and b are lengths of the legs of a right triangle and if c is the length of the hypotenuse, then
Two of the most common errors students make as they become accustomed to using the Pythagorean theorem are thinking that a + b = c, and forgetting that the sum of
is the square of the length c. You can lessen the likelihood of each of these errors by sketching a diagram such as the one in the first figure, with numbers substituted for the numbers in the problem you're working. This diagram helps focus your attention on the relationship between the side lengths of the triangle and the areas of the squares.
Eighth graders learn a proof of the Pythagorean theorem. The next figure shows two big squares with the same area.
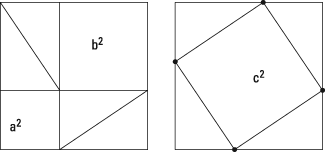
Each of these big squares is subdivided into four congruent right triangles and some other stuff. In the big square on the left, things are arranged so that the other stuff consists of a square on each leg of the right triangle. In the big square on the right, the other stuff consists of a square on the hypotenuse. The conclusion is that the two squares on the legs have the same combined area as the square on the hypotenuse, so
The key to this proof is that the only thing special about the triangles is that they're right triangles.
The converse of a theorem in math isn't generally true, but the converse of the Pythagorean theorem is true. The Pythagorean theorem starts with a right triangle and concludes that the side lengths have the relationship
The converse starts with a triangle whose sides have the relationship
and concludes that the triangle is right.
One final word about the Pythagorean theorem: The relationship
is not true for triangles that aren't right triangles. Instead, if the largest angle in a triangle is acute, then the sum of the areas of the squares with side lengths a and b will be greater than the area of the square with side length c.
and if it's an obtuse angle, then the opposite is true. The sum of the areas of the first two squares will be less than the area of the third one.
(as you can see in the next figure).