In Common Core math, sixth grade students learn to find areas of a variety of polygons by relating to the areas of known figures — especially rectangles.
You may remember from your days in school the study of area as being about long lists of unrelated formulas — one formula for triangles, another for parallelograms, and a really strange one for trapezoids. A major goal of the measurement strand in Common Core is for students to be able to relate these formulas to each other so that they can understand area and can remember (or figure out) these formulas when they are needed.
Area all goes back to rectangles. The area of a rectangle is equal to the product of the rectangle's width and length. That is, for a rectangle,
Imagine a grid of square units filling up the rectangle, and this imaginary grid has l rows with w square units in each row. So,
represents l groups of w. That meaning is important to the study of area.
A right triangle is half of a rectangle, as shown in the figure.
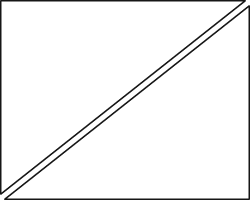
So, for right triangles,
For all triangles, not just right triangles, you can relate the area to the area of a rectangle. Typically, you use the terms base and height instead of length and width, so the formula for area of a triangle is
The reason is that the height of a triangle usually isn't the same as a side length. In the case of a rectangle, the base and height are the same as the side lengths, so base and height are terms that always work, while length and width are only useful for rectangles.
You sometimes have to be clever though and cut one of the triangles apart to see that two triangles make a rectangle with the same base and height as the triangle, as the next figure shows.
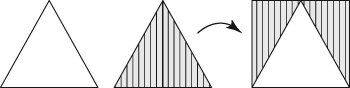
Sixth graders also find the formula for area of a parallelogram based on formulas they already know. It may involve relating parallelograms to rectangles or knowing that two identical non‐right triangles make a parallelogram, as shown in the next figure.
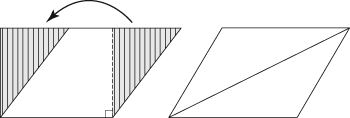
In either case, they find that for parallelograms,
Finally, sixth graders cut polygons into triangles and find the areas of the individual triangles in order to find the areas of polygons for which they don't have formulas.

