While we often think of fractions as "parts of numbers" they're also numbers themselves. Because fractions are numbers, you can compare them. Comparing fractions is an important skill in fourth grade Common Core math.
Some numbers are larger than others; children learn this early on. So asking which of two fractions is larger and putting two sets of fractions in order are sensible tasks.
Compare denominators
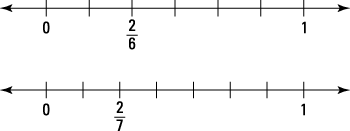
The standard way to compare two fractions is to find equivalent fractions that have the same denominator. To compare
and
you would rewrite them both as sixths:
and
Because these two fractions are built of sixths, the fraction with the larger numerator is the larger fraction, so
and therefore
as this figure demonstrates.
Compare numerators
Your child may think about this comparison differently, so the following is one more way children often compare fractions — a way that likely comes up in a Common Core classroom.
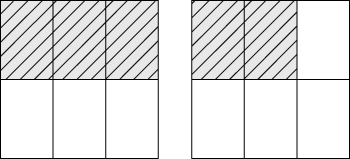
You can compare fractions using common numerators. In this way of thinking, you don't need to change the forms of
and
in order to compare them. With each of these fractions, you have one piece. The question to think about is "How big are the pieces?" If you partition something into two equal pieces, you have bigger pieces than if you partition the same thing into three equal pieces. Partitioning into two equal pieces means each piece is
of the original whole. Partitioning into three equal pieces means each piece is
of the original whole. Therefore
A more complicated example could be comparing
and
using common numerators. You can rewrite
as
so that it has a 2 in the numerator just like
does. Sixths are bigger than sevenths, so
and so
The next figure shows this problem on the number lines.