You will need to be able to measure yield for your Six Sigma initiative. In the simplest terms, a process or characteristic can either meet or not meet its specification. Just as when you harvest the fruit from an apple tree, the yield of a characteristic or process relates to how much good stuff — performance within specifications — you get out.
Traditional yield: Output versus input
Traditionally, yield is the proportion of correct items (conforming to specifications) you get out of a process compared to the number of raw items you put into it.
The traditional calculation of yield is often employed on the final inspection step of a process to measure the effectiveness of the overall process. So for the process of inflating the tires on cars in an assembly line, a study may reveal that of the 352 cars that went through the tire-inflation process during a day’s production, 347 were later found to have a pressure within the required specification limits.
In this case, the traditional yield is
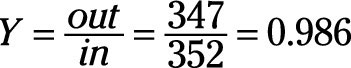
or 98.6 percent.
You can convert from a proportion such as 0.986 to perhaps a more familiar percentage scale by simply multiplying the proportion by 100. To go from percentage back to proportion, divide the percentage by 100. Just remember to always perform mathematical operations on proportions, not on percentages.
The Six Sigma perspective: First time yield (FTY)
The results of calculating yield the traditional way are misleading because they don’t account for the intricacies of the process. The calculation known as first time yield (FTY) is often much different than traditional yield. That’s because, unlike traditional yield, it captures the harsh reality of the effectiveness of the process.
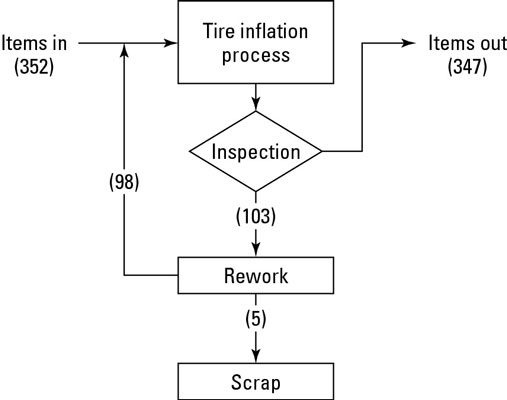
After inflation, the tire is immediately inspected to make sure it meets the required pressure specification limits. In the example, 103 tires are detected that don’t comply with the pressure specification.
Of course, the operators of the process reviewed each of these 103 and corrected (or reworked) 98 of them, leaving only five that they couldn’t bring back within the correct pressure range and had to scrap. With this detailed information, you now know that the proportion of tires going through the inflation process correctly the first time is
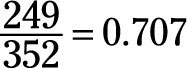
or 70.7 percent
How to uncover the hidden factory
The hidden factory is a natural outgrowth of a system’s inability to correctly comply with required specifications the first time through the process. Here and there throughout organizations, rework and fix practices arise and become engrained as “that’s just the way we do it” parts of the standard practices. But if you measure yield by using the first-time yield method you naturally objectively review and acknowledge process effectiveness.
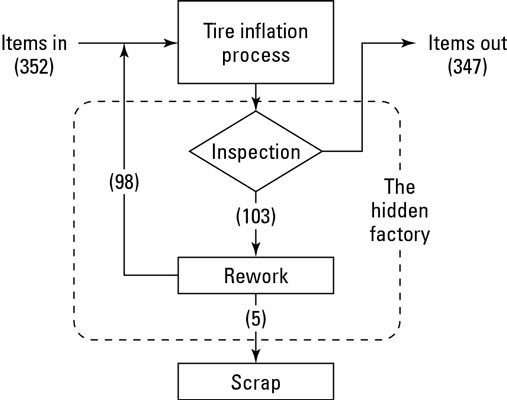
In the case of the example tire-inflation process, the hidden factory of in-process inspection and rework accounts for 0.986 – 0.707 = 0.279 or 27.9 percent of production. All together, value-sapping hidden factories within organizations combine to consume valuable resources and time.
Rolled throughput yield (RTY)
In reality, individual process steps — such as the tire-inflation example in the previous section — are strung together to create an overall process structure for accomplishing complex tasks. One way Six Sigma quantifies the complexity of a system is to count the number of processes involved.
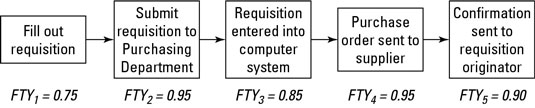
How do you calculate the overall yield for a string of processes? You multiply the first time yields for each step together, creating what is called the rolled throughput yield (RTY). For the purchase order example, the rolled throughput yield for this five-step process is
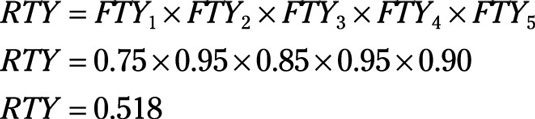
That means that the chance of a purchase order going through the process the first time with no rework or scrap is only 51.8 percent! (The last “confirmation” step in the process acts as a final test. This last step has a 90-percent yield, so you know a lot of hidden factory stuff must be going on to drop the RTY to 51.8 percent.)
You can simplify the formula for rolled throughput yield as
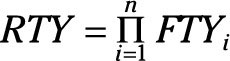
where the capital Greek letter pi (Π) tells you to multiply all the first time yields of the system together.
Even if the first time yields of the individual process steps are high, if the overall process becomes more and more complex, the system rolled throughput yield will continue to erode. Figure 13-5 charts how complexity degrades rolled throughput yield for different levels of individual first time yield.
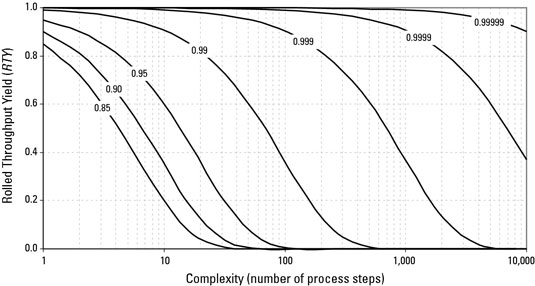
For very complex systems — such as automobiles, aircraft, data switching systems, enterprise-level business processes, and so on — a very high individual first time yield must be achieved in order to have any hope of an acceptable rolled throughput yield.

