One concept that can be applied to any expenditure or investment is generally applied to evaluations of the success of investment portfolio managers. These evaluations involve (surprise, surprise) the actual returns, risk, and average market returns. As with evaluating the estimated price and value of assets compared to the market, the degree of success is also evaluated in such a manner.
Besides seeing a trend in gradually increasing complication between the ratios described here, you may also notice that they’re all very similar with subtle but important differences. There are tons more ratios that work on the same basic premise, with each one utilizing certain measures, expectations, parameters, probabilities, and more.
With a little bit of math savvy, you could easily create your own equation that’s some slight variation of an existing one and then name it after yourself.
Ratio alpha
To understand some of these analyses, you really need to begin with the ratio α (alpha). This is calculated as follows:
αs = Rs – [Rf + βs(Rm – Rf)]
You start with the actual returns on an investment, and then subtract the value of the investment as calculated by the CAPM model. What this tells you, then, is that alpha is equal to the amount of returns generated over the market anticipated returns based on the level of risk over the market average returns (usually measured using some related index or other benchmark) and the risk-free rate.
If you anticipated returns of $100 on an investment and you generated $101, then your alpha would be $1, because you generated returns of $1 over the CAPM anticipated rate.
It’s very common for hedge fund managers and other portfolio managers to be evaluated on their ability to generate a consistently high alpha value on a given portfolio, or some variation of alpha. In fact, the amount these managers are paid is often based on alpha, a variation of alpha, or some equation that incorporates alpha.
Sharpe ratio
The Sharpe ratio is another way to look at the returns of an investment or portfolio. Rather than measuring just the amount of returns over the CAPM model, the Sharpe ratio actually measures the amount of returns for each unit of volatility that’s generated in a portfolio. In other words, higher returns and lower volatility mean more returns per unit of volatility. Here’s how it’s calculated:
S = [E(R – Rf)]/σ
It’s not that hard, but that little σ (sigma) still won’t look all that familiar unless you’re versed in statistics. All you need to worry about for the purposes of this book is that it’s a measure of variability. A higher σ indicates a wider dispersion among the rates of return.
Other than that, basically the equation says that any returns over the risk-free rate are divided by the amount of dispersion of those returns, to give you the Sharpe ratio. Measuring performance this way gives incentive for portfolio managers to take risk but ensure that they’re generating greater returns for the portfolio than volatility.
Yes, this measure is based on the faulty notion that volatility is the same as risk, working on the assumptions of CAPM, but whether it’s right or wrong, this is the Sharpe ratio.
Sterling ratio
The Sterling ratio is very similar to the Sharpe ratio, but instead of measuring risk using dispersion of returns, it measures risk using the average drawdown of the portfolio. Drawdown is an economic term that means a decline from peak performance. The Sterling ratio is calculated very simply as follows:
SR = (Rp – Rf)/Average drawdown
So, you take all the major drawdowns (losses of value) of the portfolio, add them together, and then divide the sum by the number of drawdowns. This calculation, as a result, rewards risk of lost value but only if the returns on investment are higher than the risk incurred.
V2 ratio
The V2 ratio is another ratio that works on a similar premise. This one is even slightly more complicated:
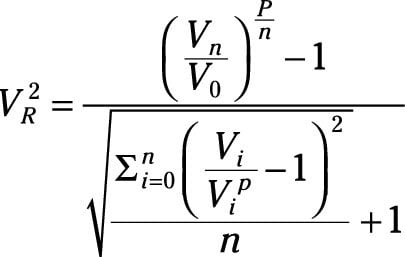
Put simply, this equation is very similar to the Sterling ratio, but it utilizes drawdowns in excess of market drawdowns measured by the average drawdowns of some benchmark index.

