Collections of individual assets interact together to influence the overall portfolio. So when several investments are lumped together in a portfolio, every single investment has an influence on the portfolio.
Think of it like this: Envision a ring that’s held up by several rubber bands tied to it. Each rubber band acts like a single investment, so that the location of the ring in the middle is determined by the length of each rubber band.
Now, if you pull on one of those rubber bands, the ring doesn’t move as much as the rubber band because the ring is still being held somewhat in place by the other rubber bands.
The figure illustrates something called the efficient frontier. The linear line labeled “Best possible CAL” illustrates the best potential proportion of returns to risk. CAL stands for capital allocation line, which means that any optimized portfolio will fall on that line.
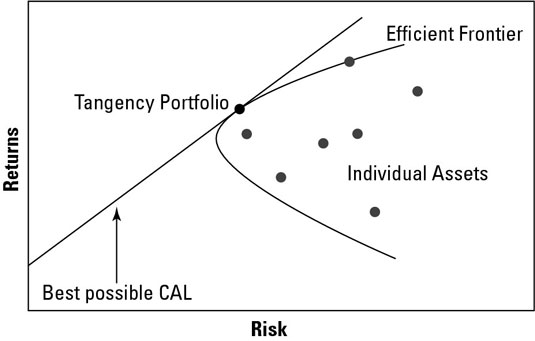
The contradiction is that the individual assets will not fall on that line, so you have to use diversification of your portfolio to make it happen. Because investments that change value in opposite directions reduce risk below the risk of any individual asset through diversification, it’s possible to decrease the total risk of a portfolio, shifting it to the left, at any given rate of return.
The efficient frontier is the maximum amount of returns that can be generated for a given level of risk in a portfolio. The portfolio is optimized at the point of tangency, where the efficient frontier intersects the best possible CAL using a given investment portfolio. The dot where the lines intersect shows the point of an optimized portfolio generated using the individual investments illustrated by the solid dots.
How can you ensure that you’re doing this, though? How can you measure these influences that individual investments have on the risk and return of the whole portfolio? Again, you use math!
According to CAPM, you measure the returns of a portfolio like this:
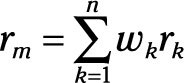
This equation says that the returns on a portfolio are the sum of the returns of the individual investments weighted by the proportion of their contribution to the portfolio. Here’s a quick example to illustrate. Assume the following facts about Investments A, B, and C:
Investment A: 10% returns, 50% portfolio
Investment B: 5% returns, 25% portfolio
Investment C: 0% returns, 25% portfolio
So, you calculate the returns on the portfolio like this:
10%(0.5) + 5%(0.25) + 0%(0.25) = 5% + 2.5% + 0% = 7.5%
According to CAPM, you measure risk (remember that risk is defined by CAPM as volatility rather than actual risk) like this:
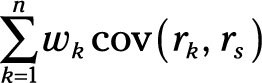
This equation works just like the portfolio returns under CAPM, except it uses the weighted sum of covariances of the individual investments. In contrast, the portfolio variability under APT is calculated as follows:
Σwiβi
Once again, you use the sum of weighted variability, but this time you measure the variability of the individual factors influencing the individual investments. Doing this calculation allows you to input the value into another equation that measures the portfolio returns under APT:
rp = E(rp) + βp + εp
Here, the returns on the portfolio are the expected portfolio returns while also accounting for the portfolio variability and any short-term market shocks influencing price.
The question becomes whether or not all this math is worth the effort or whether you should simply invest in a passively-managed index portfolio that matches an asset index (there are indices of stocks, bonds, derivative investments, and all sorts of stuff).
The truth is that the vast majority of portfolios consistently generate fewer returns in the long run than index-matched portfolios. If anyone were to develop and announce a better method of portfolio management than the efficient market hypothesis, the rest of the market would adopt the new method, eliminating the ability of the inventor to continue making money using that method.
So, it should come as no surprise that anyone who has a better method isn’t going to tell you about it.
A big part of professional portfolio management that allows some investors to generate above-normal returns has come from technology. Asset trades are now measured in milliseconds, so that the person with the fastest automated transactions is able to generate the most returns by simply making a purchase before the price is driven up by other investors or selling before the price is driven down.
Although effective, this advantage speaks more to these investors’ expertise in technology than in finance.
Another look at these above-normal returns in a portfolio shows that many of the successful portfolios actually lose their gains during an economic downturn. Remember that trade-off between risk and return?
Well, investing is easy when the economy is growing because just about everything is doing well. Portfolio managers will take on extra risk to gain those extra returns, but when the economy starts to slump, all those gains disappear. This drawback can be mitigated by carefully watching the national economy and taking the following precautions when indicators start pointing toward a downturn:
Start buying options
Start selling some of your portfolio
Transition to lower-risk investments
Continue to take risk by short-selling assets.
In any case, it’s quite possible to avoid the loss that high-risk portfolios bring during a recession in contrast to the gains they make during an economic boom. But you need to take precautions and develop a keen mind for macroeconomics.
New innovations for portfolio management crop up all the time: new calculations, new models, new advances in mathematics and statistics, and new technologies. There are new and better ways to measure risk, find combinations of factors that influence APT calculations, and identify more accessible markets.
The overriding goal is to better utilize the synergy between assets to maximize the returns that corporate investments yield while limiting the amount of risk they’re exposed to. When you start talking about a corporation’s money, tons of energy and resources go into finding new innovations to generate better returns on investment, regardless of the type of assets in which the corporation is investing.

