An exponential function is when the independent variable is in the exponent of a constant. The base of the function must be greater than 0 and not equal to 1. Some examples of exponential functions are:
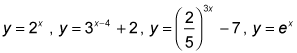
If the base of the exponential function is a fraction, then the graph falls rapidly to the right, as shown here.
Looking for these general shapes when given a graph will indicate whether the graph represents an exponential function.
If you're given a table, to determine whether the function is exponential, check if there's a common multiple difference, meaning you can multiply each of the y-values by a number to get to the next y-value. This indicates that the function is exponential and, in fact, that that number is your base.
To write an equation for an exponential function, follow these steps:
- Find the common multiple difference (this is your base, b).
- Find your y-intercept—this is the coefficient of your exponential function (a).
- Substitute your values for a and b into the general form of an exponential:
For example:
First find whether there's a common multiple difference. It's important to note that the x-values are evenly spaced, which allows the common multiple to be identifiable.
You now know that your base is 2. Looking for your y-intercept, you see it's (0, 3), so a = 3. Now substitute these values into









