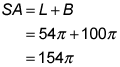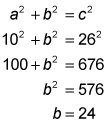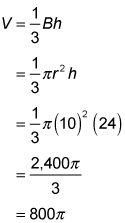As you'll see in the following practice questions, you may be asked to calculate a cone's surface area (in this case, based on its lateral area and base area) or its volume (in this case, given its radius and slant height).
Practice questions
- A cone has a lateral area of and a base area of
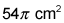 .
.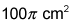
How many square centimeters is the surface area of the cone?
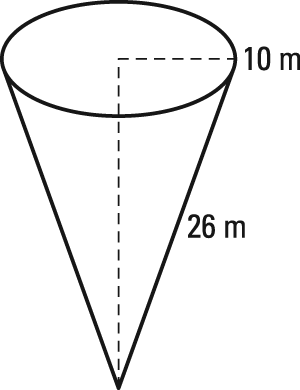
Refer to the following figure for the next question.
- What is the volume of the cone?
Answers and explanations
- The correct answer is Choice (E).
The surface area of a cone is the sum of its lateral area (L) and base area. A cone has only one base, so you add B to the lateral area instead of 2B.
The surface area of the cone is
- The correct answer is Choice (B).
The volume of a cone is a third of the product of its base and its height. The height of this cone isn't given, but you can use the Pythagorean theorem to find it. The height, a radius, and the slant height form a right triangle in which the height and the radius are perpendicular and the slant height is the hypotenuse.
The height of the cone is 24 m. That times a third of the base area is the volume of the cone:
The volume of the cone is