As when solving an ACT Math problem that includes an expression with absolute value, you also need to split an inequality with absolute value into two separate inequalities. However, keep in mind one twist: One of the two resulting inequalities is simply the original inequality with the bars removed. The other inequality is the original inequality with
The bars removed
The opposite side negated (as with absolute value equations)
The inequality reversed (as with inequalities when you multiply or divide by a negative number)
These rules aren’t difficult, but they’re a little complicated, so be careful to do all three parts correctly.
Example 1
Which of the following values is in the solution set of
(A) 0
(B) 2
(C) –2
(D) 4
(E) –4
Begin by splitting the inequality:
Notice that the second of these two inequalities has the bars removed, the right side negated, and the inequality sign reversed. You’re now ready to solve both of these inequalities for t:
To make these inequalities a little easier to read, put them in the following form:
Thus, 0 falls into the range of solutions, so the right answer is Choice (A).
In some cases, the solution to an inequality with absolute value can lead to a pair of inequalities that appear to contradict each other. When this happens, both inequalities aren’t true, but at least one of them is, so link them with the word or. This concept is a little tricky, so don’t worry if it’s not making sense. The next problem provides a concrete example.
Example 2
What is the solution set for

Before you begin, notice that the original inequality is
so no solution can include either
As a result, you can rule out Choices (G) and (J). Now isolate
on the left side of the inequality:
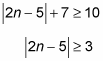
You’re now ready to remove the bars and split the inequality:
Notice that the second of these two inequalities has the bars removed, the right side negated, and the inequality sign reversed. You’re now ready to solve the first one:
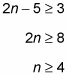
Next, solve the second inequality:
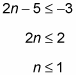
Notice that the two solutions
seem to contradict each other: If n is greater than 4, how can it be less than 1? When this situation occurs, either solution can be true, so link the two resulting solutions with the word or:
Thus, the correct answer is Choice (K).
Be extra careful when working with an inequality that sets an absolute value either greater than or greater than or equal to another value that includes a variable. This type of inequality can sometimes produce a false (or extraneous) solution — that is, a solution that appears correct but doesn’t work when plugged back into the problem. The next example shows you how and why this can happen.
Which of the following is the solution set for
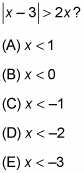
To begin, remove the absolute value bars, split the inequality, and solve each separately:
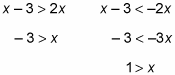
According to this result, x x x = 0 should be outside the solution set. So plugging 0 into the original inequality should give you the wrong answer:
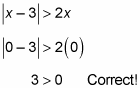
This solution is unexpected. In fact, x = 0 is in the solution set for this inequality.
What went wrong? Take another look at the original inequality:
This inequality sets an absolute value greater than 2x. So if x is any negative number, the absolute value (which can never be negative) must be in the solution set. Therefore, the solution x x are in the solution set. Throwing out this false solution leaves you with the correct answer, which is x





