Electronics is more than just schematics and circuits. By using various components, such as resistors and capacitors, electronics allows you to bend electric current to your will to create an infinite variety of gizmos and gadgets. In exploring electronics, use this handy reference for working with Ohm’s, Joule’s, and Kirchhoff’s Laws; making important calculations; determining the values of resistors and capacitors according to the codes that appear on their casings; and using a 555 timer and other integrated circuits (ICs).
Important Formulas in Electronics
With just a handful of basic mathematical formulas, you can get pretty far in analyzing the goings-on in electronic circuits and in choosing values for electronic components in circuits you design.
Ohm’s Law and Joule’s Law
Ohm’s Law and Joule’s Law are commonly used in calculations dealing with electronic circuits. These laws are straightforward, but when you’re trying to solve for one variable or another, it is easy to get them confused. The following table presents some common calculations using Ohm’s Law and Joule’s Law. In these calculations:
V = voltage (in volts)
I = current (in amps)
R = resistance (in ohms)
P = power (in watts)
| Unknown Value | Formula |
|---|---|
| Voltage | V = I x R |
| Current | I = V/R |
| Resistance | R = V/I |
| Power | P = V x I or P = V2/R or P = I2R |
Equivalent resistance and capacitance formulas
Electronic circuits may contain resistors or capacitors in series, parallel, or a combination. You can determine the equivalent value of resistance or capacitance using the following formulas:
Resistors in series:
Resistors in parallel:
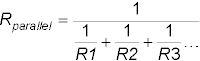
or
Capacitors in series:
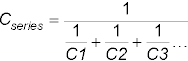
or
Capacitors in parallel:
Kirchhoff’s Current and Voltage Laws
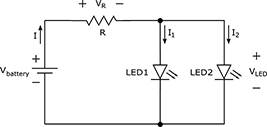
Kirchhoff’s Circuit Laws are commonly used to analyze what’s going on in a closed loop circuit. Based on the principle of conservation of energy, Kirchhoff’s Current Law (KCL) states that, at any node (junction) in an electrical circuit, the sum of currents flowing into that node is equal to the sum of currents flowing out of that node, and Kirchhoff’s Voltage Law (KVL) states that the sum of all voltage drops around a circuit loop equals zero.
For the circuit shown, Kirchhoff’s Laws tells you the following:
KCL: I = I1 + I2
KVL: Vbattery – VR – VLED = 0, or Vbattery = VR + VLED
Calculating the RC time constant
In a resistor-capacitor (RC) circuit, it takes a certain amount of time for the capacitor to charge up to the supply voltage, and then, once fully charged, to discharge down to 0 volts.
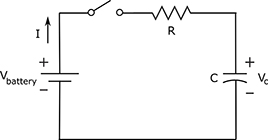
Circuit designers use RC networks to produce simple timers and oscillators because the charge time is predictable and depends on the values of the resistor and the capacitor. If you multiply R (in ohms) by C (in farads), you get what is known as the RC time constant of your RC circuit, symbolized by T:
A capacitor charges and discharges almost completely after five times its RC time constant, or 5RC. After the equivalent of one time constant has passed, a discharged capacitor will charge to roughly two-thirds its capacity, and a charged capacitor will discharge nearly two-thirds of the way.
Electronics: Reading Resistor and Capacitor Codes
Electronics can sometimes be difficult to decipher. By decoding the colorful stripes sported by many resistors and the alphanumeric markings that appear on certain types of capacitors, you can determine the nominal value and tolerance of the specific component.
Resistor color codes
Many resistor casings contain color bands that represent the nominal resistance value and tolerance of the resistor. You translate the color and position of each band into digits, multipliers, and percentages.
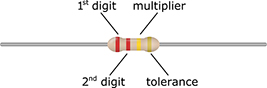
The table that follows outlines the meaning of the resistor color bands.
| Color | 1st Digit | 2nd Digit | Multiplier | Tolerance |
|---|---|---|---|---|
| Black | 0 | 0 | x1 | ±20% |
| Brown | 1 | 1 | x10 | ±1% |
| Red | 2 | 2 | x100 | ±2% |
| Orange | 3 | 3 | x1,000 | ±3% |
| Yellow | 4 | 4 | x10,000 | ±4% |
| Green | 5 | 5 | x100,000 | n/a |
| Blue | 6 | 6 | x1,000,000 | n/a |
| Violet | 7 | 7 | x10,000,000 | n/a |
| Gray | 8 | 8 | x100,000,000 | n/a |
| White | 9 | 9 | n/a | n/a |
| Gold | n/a | n/a | x0.1 | ±5% |
| Silver | n/a | n/a | x0.01 | ±10% |
Capacitor value reference
In electronic circuits, the value of a capacitor can be determined by a two- or three-digit code that appears on its casing. The following table outlines values for some common capacitors.
| Marking | Value |
|---|---|
| nn (a number from 01 to 99) or nn0 | nn picofarads (pF) |
| 101 | 100 pF |
| 102 | 0.001 µF |
| 103 | 0.01 µF |
| 104 | 0.1 µF |
| 221 | 220 pF |
| 222 | 0.0022 µF |
| 223 | 0.022 µF |
| 224 | 0.22 µF |
| 331 | 330 pF |
| 332 | 0.0033 µF |
| 333 | 0.033 µF |
| 334 | 0.33 µF |
| 471 | 470 pF |
| 472 | 0.0047 µF |
| 473 | 0.047 µF |
| 474 | 0.47 µF |
Capacitor tolerance codes
In electronic circuits, the tolerance of capacitors can be determined by a code that appears on the casing. The code is a letter that often follows a three-digit number, for instance, the Z in 130Z. The following table outlines common tolerance values for capacitors. Note that the letters B, C, and D represent tolerances in absolute capacitance values, rather than percentages. These three letters are used on only very small (pF range) capacitors.
| Code | Tolerance |
|---|---|
| B | ± 0.1 pF |
| C | ± 0.25 pF |
| D | ± 0.5 pF |
| F | ± 1% |
| G | ± 2% |
| J | ± 5% |
| K | ± 10% |
| M | ± 20% |
| Z | +80%, –20% |
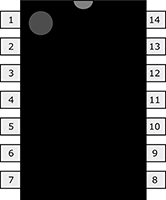
Electronics: Integrated Circuit (IC) Pinouts
The pins on an IC chip provide connections to the tiny integrated circuits inside of your electronics. To determine which pin is which, you look down on the top of the IC for the clocking mark, which is usually a small notch in the packaging but might instead be a little dimple or a white or colored stripe. By convention, the pins on an IC are numbered counterclockwise, starting with the upper-left pin closest to the clocking mark. So, for example, with the clocking notch orienting the chip at the 12 o’clock position, the pins of a 14-pin IC are numbered 1 through 7 down the left side and 8 through 14 up the right side.
Electronics: 555 Timer as an Astable Multivibrator
The 555 can behave as an astable multivibrator, or oscillator. By connecting components to the chip in your electronics, you can configure the 555 to produce a continuous series of voltage pulses that automatically alternate between low (0 volts) and high (the positive supply voltage, VCC).
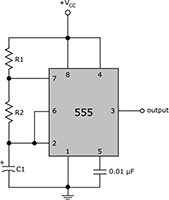
You can calculate the low and high timing intervals using the formulas that follow:

