When using variable substitution to evaluate a definite integral, you can save yourself some trouble at the end of the problem. Specifically, you can leave the solution in terms of u by changing the limits of integration.
For example, suppose that you’re evaluating the following definite integral:
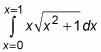
Notice that this example gives the limits of integration as x = 0 and x = 1. This is just a notational change to remind you that the limits of integration are values of x. This fact becomes important later in the problem.
You can evaluate this equation simply by using variable substitution:
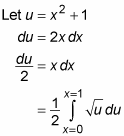
If this were an indefinite integral, you’d be ready to integrate. But because this is a definite integral, you still need to express the limits of integration in terms of u rather than x. Do this by substituting values 0 and 1 for x in the substitution equation u = x2 + 1:
u = 12 + 1 = 2
u = 02 + 1 = 1
Now use these values of u as your new limits of integration:
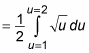
At this point, you’re ready to integrate:
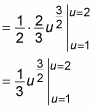
Because you changed the limits of integration, you can now find the answer without switching the variable back to x:







