Multiplying a vector by a scalar is called scalar multiplication. To perform scalar multiplication, you need to multiply the scalar by each component of the vector.
A scalar is just a fancy word for a real number. The name arises because a scalar scales a vector — that is, it changes the scale of a vector. For example, the real number 2 scales the vector v by a factor of 2 so that 2v is twice as long as v.
Here’s how you multiply the vector
For example, you multiply the vector
by the scalars 2, –4, and 1/3 as follows:
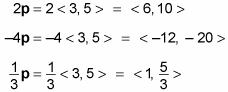
When you multiply a vector by a scalar, the result is a vector.
Geometrically speaking, scalar multiplication achieves the following:
Scalar multiplication by a positive number other than 1 changes the magnitude of the vector but not its direction.
Scalar multiplication by –1 reverses its direction but doesn’t change its magnitude.
Scalar multiplication by any other negative number both reverses the direction of the vector and changes its magnitude.
Scalar multiplication can change the magnitude of a vector by either increasing it or decreasing it.
Scalar multiplication by a number greater than 1 or less than –1 increases the magnitude of the vector.
Scalar multiplication by a fraction between –1 and 1 decreases the magnitude of the vector.
 Scalar multiplication of a vector changes its magnitude and/or its direction.
Scalar multiplication of a vector changes its magnitude and/or its direction.
For example, the vector 2p is twice as long as p, the vector 1/2 p is half as long as p, and the vector –p is the same length as p but extends in the opposite direction from the origin (as shown here).






