Every whole number greater than 1 has a prime factorization — that is, the list of prime numbers (including repeats) that equal that number when multiplied together. For example, here are the prime factorizations of 14, 20, and 300:
14 = 2 × 7
20 = 2 × 2 × 5
300 = 2 × 2 × 2 × 3 × 5
Factor trees are a useful tool for finding the prime factorization of a number. For example, to find the prime factorization 30, first find a factor pair — a pair of numbers that, when multiplied together, equals 30:
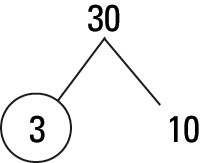
Note that 3 is circled because it's a prime number. But 10 is not prime, so you can continue the tree, finding a factor pair for 10:
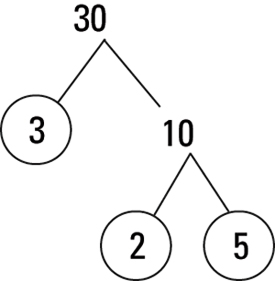
This time, both 2 and 5 are circled because they're each prime numbers. When the bottom numbers on the factor tree are all prime, you have your answer: 30 = 2 × 3 × 5.
Using prime factorization to find the GCF
You can use prime factorization to find the greatest common factor (GCF) of a set of numbers. This method often works better for large numbers, when generating lists of all factors can be time-consuming.
Here's how to find the GCF of a set of numbers, using prime factorization:
List the prime factors of each number.
Circle every common prime factor — that is, every prime factor that's a factor of every number in the set.
Multiply all the circled numbers.
The result is the GCF.
For example, suppose you want to find the GCF of 28, 42, and 70. Step 1 says to list the prime factors of each number. Step 2 says to circle every prime factor that's common to all three numbers:
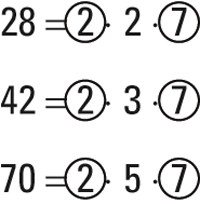
As you can see, the numbers 2 and 7 are common factors of all three numbers, so multiply these two numbers as follows:
2 × 7 = 14
Thus, the GCF of 28, 42, and 70 is 14.
Knowing how to find the GCF of a set of numbers is important when you begin reducing fractions to lowest terms.
Using prime factorization to find the LCM
One method for finding the least common multiple (LCM) of a set of numbers is to use the prime factorizations of those numbers. Here's how:
List the prime factors of each number.
Suppose you want to find the LCM of 18 and 24. List the prime factors of each number:
18 = 2 × 3 × 3
24 = 2 × 2 × 2 × 3
For each prime number listed, underline the most repeated occurrence of this number in any prime factorization.
The number 2 appears once in the prime factorization of 18 but three times in that of 24, so underline the three 2s:
18 = 2 × 3 × 3
24 = 2 × 2 × 2 × 3
Similarly, the number 3 appears twice in the prime factorization of 18 but only once in that of 24, so underline the two 3s:
18 = 2 × 3 × 3
24 = 2 × 2 × 2 × 3
Multiply all the underlined numbers.
Here's the product:
2 × 2 × 2 × 3 × 3 = 72
So the LCM of 18 and 24 is 72. This solution checks out because
18 × 4 = 72
24 × 3 = 72

