In physics, no force can be exerted without an equal and opposite force (even if some of that opposing force comes from making an object accelerate). A rope and pulley can act together to change the direction of the force you apply, but not for free. In order to change the direction of your force from –F (that is, downward) to +F (upward on the mass), the pulley’s support has to respond with a force of 2F.
Here’s how this works: When you pull a rope in a pulley system to lift a stationary object, you lift the mass if you exert enough force to overcome its weight, mg, where g is the acceleration due to gravity at the surface of the Earth, 9.8 meters/second2. Take a look at the figure, in which a rope goes over a pulley and down to a mass m.
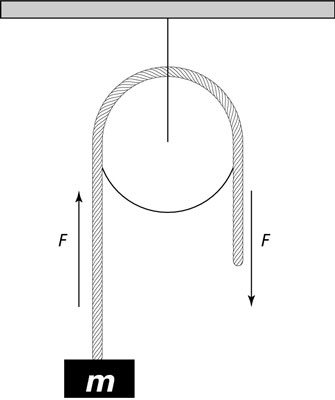
The rope and pulley together function not only to transmit the force you exert, F, but also to change the direction of that force, as you see in the figure. The force you exert downward is exerted upward on the mass, because the rope, going over the pulley, changes the force’s direction. In this case, if F is greater than mg, you can lift the mass. If you apply no force on the object (meaning there’s no tension in the rope), then the only force acting on it is gravity, Fgravity, and so the object falls freely and accelerates at a rate of –g (the negative sign indicates that the acceleration is downward) because
If you apply a force on the rope of magnitude F, then it is transmitted by the rope and pulley to the object as an upwardly directed force of the same magnitude. Therefore, the total force on the object is given by the sum of these two forces,
By Newton’s second law, the sum of the forces on a mass is equal to ma. So, if the force you apply by pulling down on the rope is greater than the weight of the object (mg), then the object will accelerate upward.
The force F, acting alone without gravity, would accelerate the object upward at a rate that you can call a:
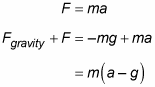
So you can see that if F is greater than mg, then a is greater than g and the object accelerates upward.
But this force-changing use of a rope and pulley comes at a cost, because you can’t cheat Newton’s third law. Assume that you lift the mass and it hangs in the air. In this case, F must equal mg to hold the mass stationary. The direction of your force is being changed from downward to upward. How does that happen?
To figure this out, consider the force that the pulley’s support exerts on the ceiling. What’s that force? Because the pulley isn’t accelerating in any direction, you know that
on the pulley. That means that all the forces on the pulley, when added up, give you zero.
From the pulley’s point of view, two forces pull downward: the force F you pull with and the force mg that the mass exerts on you (because nothing is moving at the moment). That’s 2F downward. To balance all the forces and get 0 total, the pulley’s support must exert a force of 2F upward.

