In physics, Pascal’s principle says that given a fluid in a totally enclosed system, a change in pressure at one point in the fluid is transmitted to all points in the fluid, as well as to the enclosing walls. In other words, if you have a fluid enclosed in a pipe (with no air bubbles) and change the pressure in the fluid at one end of the pipe, the pressure changes all throughout the pipe to match.
The fact that pressure inside an enclosed system is the same (neglecting gravitational differences) has an interesting consequence. Because P = F/A, you get the following equation for force:
F = PA
So if the pressure is the same everywhere in an enclosed system but the areas you consider are different, can you get different forces?
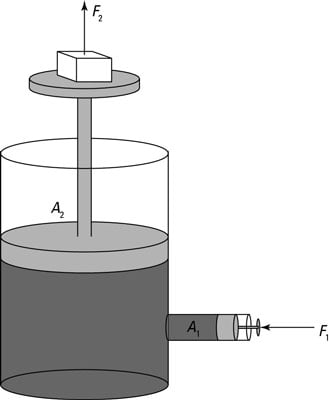
To make this question clearer, look at the figure, which shows a system of enclosed fluid with two hydraulic pistons, one with a piston head of area A1 and one with a piston head of area A2. You apply a force of F1 on the smaller piston. What is the force on the other piston, F2?
Pressure at each point is F/A. According to Pascal’s principle, the pressure is the same everywhere inside the fluid, so:
Solving for F2 gives you the force at Point 2:
That means that you can develop a huge force from a small force if the ratio of the piston sizes is big. For example, say the area of Piston 2 is bigger than Piston 1 by a factor of 100. Does that mean that any force you apply to piston 1 will be multiplied by 100 times on piston 2?
Yes, indeed — that’s how hydraulic equipment works. By using a small piston at one end and a large piston at the other, you can create huge forces. Backhoes and other hydraulic machines, such as garbage trucks and hydraulic lifts, use Pascal’s principle to function.
What’s the catch here? If you push on Piston 1 and get 100 times the force on Piston 2, you seem to be getting something for nothing. The catch is that you have to push the smaller piston 100 times as far as the second piston will move.

