The geometric series is a simplified form of a larger set of series called the power series. A power series is any series of the following form:
Notice how the power series differs from the geometric series:
In a geometric series, every term has the same coefficient.
In a power series, the coefficients may be different — usually according to a rule that’s specified in the sigma notation.
Here are a few examples of power series:
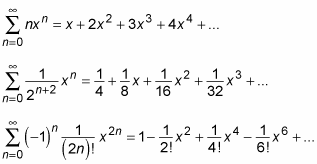
You can think of a power series as a polynomial with an infinite number of terms. For this reason, many useful features of polynomials carry over to power series.
The most general form of the power series is as follows:
This form is for a power series that’s centered at a. Notice that when a = 0, this form collapses to the simpler version:
So a power series in this form is centered at 0.

