Conduction transfers heat through material directly, through contact. Thanks to physics, we know that conduction is affected by temperature difference, the area of conduction, the distance the heat must travel, and the amount of time that passes.
Take a look at the metal pot in the figure and its metal handle; the pot has been boiling for 15 minutes. Would you want to lift it off the fire by grabbing the handle without an oven mitt? Probably not. The handle is hot because of conduction of heat through the metal handle.
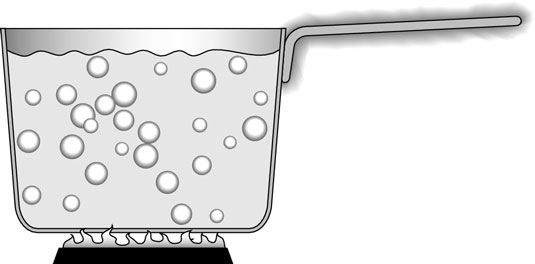
On the molecular level, the molecules near the heat source are heated and begin vibrating faster. They bounce off nearby molecules and cause them to vibrate faster. That increased bouncing is what heats a substance.
You have to take different properties of objects into account when you want to examine the conduction that takes place. If you have a bar of steel, for example, you have to consider the bar’s cross-sectional area and length, along with the temperature at different parts of the bar.
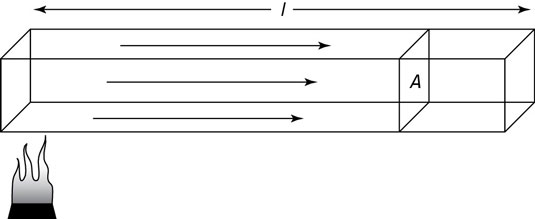
Take a look at the second figure, where a bar of steel is being heated on one end and the heat is traveling by conduction toward the other side. Can you find out the thermal energy transferred? No problem.
Here are the factors that affect the rate of conduction:
Temperature difference. The greater the difference in temperature between the two ends of the bar, the greater the rate of thermal energy transfer, so more heat is transferred. The heat, Q, is proportional to the difference in temperature:
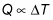
Cross-sectional area. A bar twice as wide conducts twice the amount of heat. In general, the amount of heat conducted, Q, is proportional to the cross-sectional area, A, like this:
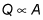
Length (distance heat must travel). The longer the bar, the less heat that will make it all the way through. Therefore, the conducted heat is inversely proportional to the length of the bar, l:
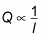
Time. The amount of heat transferred, Q, depends on the amount of time that passes, t — twice the time, twice the heat. Here’s how you express this idea mathematically:
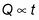
Now you can put the variables together, using k as a constant of proportionality that’s yet to be determined.
Here’s the equation for heat transfer by conduction through a material:
This equation represents the amount of heat transferred by conduction in a given amount of time, t, down a length l, where the cross-sectional area is A. Here, k is the material’s thermal conductivity, measured in joules per second-meters-degrees Celsius, or

