The Pythagorean identities pop up frequently in trig proofs. Pay attention and look for trig functions being squared. Try changing them to a Pythagorean identity and see whether anything interesting happens.
The three Pythagorean identities are
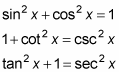
After you change all trig terms in the expression to sines and cosines, the proof simplifies and makes your job that much easier. For example, follow these steps to prove
![]()
-
Convert all the functions in the equality to sines and cosines.

-
Use the properties of fractions to simplify.
Dividing by a fraction is the same as multiplying by its reciprocal, so

-
Identify the Pythagorean identity on the left side of the equality.
Because sin2 x + cos2 x = 1, you can say that 1 = 1.






