If you use natural log values for your independent variables (X) and keep your dependent variable (Y) in its original scale, the econometric specification is called a linear-log model (basically the mirror image of the log-linear model). These models are typically used when the impact of your independent variable on your dependent variable decreases as the value of your independent variable increases.
The behavior of the function is similar to a quadratic, but it’s different in that it never reaches a maximum or minimum Y value.
The original model is not linear in parameters, but a log transformation generates the desired linearity. (Recall that linearity in parameters is one of the OLS assumptions.)
Consider the following model of consumption spending, which depends on some autonomous consumption and income:
where Y represents consumption spending,
is autonomous consumption (consumption that doesn’t depend on income), X is income, and
is the estimated effect of income on consumption.
You’re probably familiar with the relationship between income and consumption. In your principles of economics courses, you probably referred to it as an Engel curve. You may not have seen the mathematical function behind it, but you’ve seen the graphical depiction.
The estimation of consumption functions isn’t the only use of linear-log functions. Economists tend to use these functions anytime that the unit changes in the dependent variable are likely to be less than the unit changes in the independent variables.
If you begin with a function of the form
where the value of Y for a given X can be derived only if the impact is known, then you can estimate the impact using OLS only if you use a log transformation. If you take the natural log of both sides, you end up with
where
is the unknown constant and
is the unknown impact of X. You can estimate this with OLS by simply using natural log values for the independent variable (X) and the original scale for the dependent variable (Y).
After estimating a linear-log model, the coefficients can be used to determine the impact of your independent variables (X) on your dependent variable (Y). The coefficients in a linear-log model represent the estimated unit change in your dependent variable for a percentage change in your independent variable.
Using calculus with a simple linear-log model, you can see how the coefficients should be interpreted. Begin with the model
and differentiate it to obtain
The term on the right-hand-side is the percent change in X, and the term on the left-hand-side is the unit change in Y.
In economics, many situations are characterized by diminishing marginal returns. The linear-log model usually works well in situations where the effect of X on Y always retains the same sign (positive or negative) but its impact decreases.
Suppose, using a random sample of schools districts, you obtain the following regression estimates:
where Y is the average math SAT score and X is the expenditure per student. The estimated coefficient
implies that a 1 percent increase in expenditure per student increases the average math SAT score by 0.65 points.
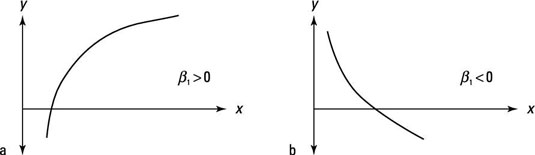
If you estimate a linear-log regression, a couple outcomes for the coefficient on X produce the most likely relationships:
Part (a) shows a linear-log function where the impact of the independent variable is positive.
Part (b) shows a linear-log function where the impact of the independent variable is negative.
As with log-log and log-linear models, the regression coefficients in linear-log models don’t represent slope.






