The last reciprocal function is the cotangent, abbreviated cot. This function is the reciprocal of the tangent (hence, the co-). The ratio of the sides for the cotangent is adjacent/opposite.
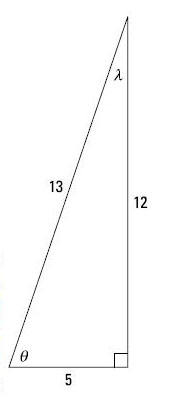
You can see that the two cotangents are
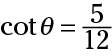
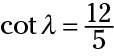
The ratio for the cotangent is just that ratio, not necessarily the lengths of the sides. The fraction made by the lengths might’ve been reduced by dividing numerator and denominator by the same number.
Sometimes you know the value of the cotangent along with other information and have to solve for one or both of the sides. Try this example: What are the lengths of the legs of a right triangle if
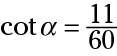
and the hypotenuse is 183 inches long?
Write the adjacent and opposite sides as multiples of the same number, m, and put them in the Pythagorean theorem with the hypotenuse.
(11m)2 + (60m)2 = 1832
Simplify the equation and solve for m.

Use the value of m to find the lengths of the two legs.
Because you know that m = 3, you know that the adjacent side is 11m = 11(3) = 33, and the opposite side is 60m = 60(3) = 180. The three sides of the right triangle are 33, 180, and 183. You can double-check your results by plugging these three numbers into the Pythagorean theorem and making sure the theorem holds true.





