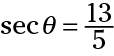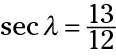The cosecant function, abbreviated csc, is the reciprocal of the sine function and thus uses this ratio: hypotenuse/opposite. The hypotenuse of a right triangle is always the longest side, so the numerator of this fraction is always larger than the denominator. As a result, the cosecant function always produces values bigger than 1.
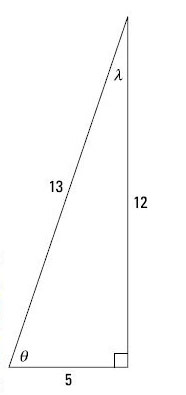
You can use the values shown to determine the cosecants of the two acute angles:
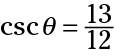
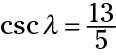
Suppose someone asks you to find the cosecant of angle alpha if you know that the hypotenuse is 1 unit long and that the right triangle is isosceles. Remember that an isosceles triangle has two congruent sides. These two sides have to be the two legs, because the hypotenuse has to have the longest side. So, to find the cosecant:
Find the lengths of the two legs.
The Pythagorean theorem says that a2 + b2 = c2, but because two sides are congruent, you can take out one variable and write the equation as a2 + a2 = c2. Put in 1 for c and solve for a.
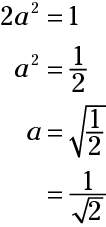
The legs are both
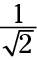
units long. You can leave the radical in the denominator and not worry about rationalizing, because you’re going to input the whole thing into the cosecant ratio, anyway, and things can change.
Use the length of the opposite side in the ratio for cosecant.
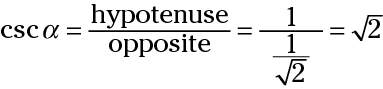
The secant function, abbreviated sec, is the reciprocal of the cosine. So, its ratio is hypotenuse/adjacent. Just as with the cosecant, the ratio of the sides is greater than 1. Using the triangle in the figure, the two secants are