In econometrics, an extremely common test for heteroskedasticity is the White test, which begins by allowing the heteroskedasticity process to be a function of one or more of your independent variables. It’s similar to the Breusch-Pagan test, but the White test allows the independent variable to have a nonlinear and interactive effect on the error variance.
Typically, you apply the White test by assuming that heteroskedasticity may be a linear function of all the independent variables, a function of their squared values, and a function of their cross products:
As in the Breusch-Pagan test, because the values for
aren’t known in practice, the
are calculated from the residuals and used as proxies for
The White test is based on the estimation of the following:
Alternatively, a White test can be performed by estimating
Follow these five steps to perform a White test:
Estimate your model using OLS:
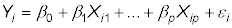
Obtain the predicted Y values after estimating your model.
Estimate the model using OLS:
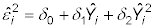
Retain the R-squared value from this regression:
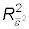
Calculate the F-statistic or the chi-squared statistic:
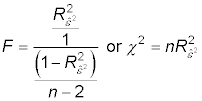
The degrees of freedom for the F-test are equal to 2 in the numerator and n – 3 in the denominator. The degrees of freedom for the chi-squared test are 2. If either of these test statistics is significant, then you have evidence of heteroskedasticity. If not, you fail to reject the null hypothesis of homoskedasticity.
Imagine that you’re estimating a model with the natural log of Major League Baseball players’ contract value as the dependent variable and several player characteristics as independent variables. When you plug this information into STATA (which lets you run a White test via a specialized command), the program retains the predicted Y values, estimates the auxiliary regression internally, and reports the chi-squared test.
The figure shows the resulting output, which suggests you should reject the homoskedasticity hypothesis.
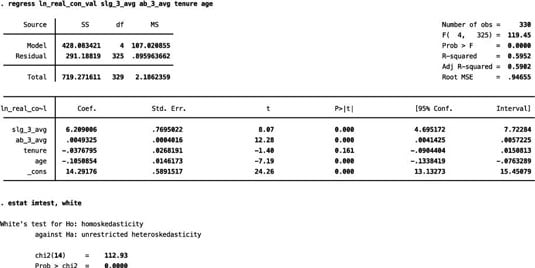
Although the White test provides a flexible functional form that’s useful for identifying nearly any pattern of heteroskedasticity, it’s not useful for determining how to correct or adjust the model for heteroskedasticity.

