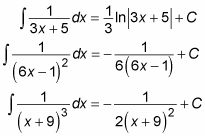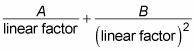
For each quadratic factor in the denominator that’s raised to the third power, add three partial fractions in the following form:
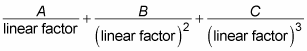
Generally speaking, when a linear factor is raised to the nth power, add n partial fractions. For example, suppose that you want to integrate the following expression:
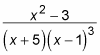
This expression contains all linear factors, but one of these factors (x + 5) is nonrepeating and the other (x – 1) is raised to the third power. Set up your partial fractions this way:
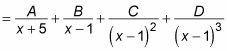
Which will yield:
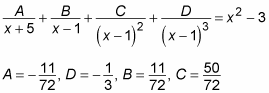
As you can see, this example adds one partial fraction to account for the nonrepeating factor and three to account for the repeating factor.
When you start out with a linear factor, using partial fractions leaves you with an integral in the following form:
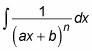
Integrate all these cases by using the variable substitution u = ax + b so that du = a dx and
This substitution results in the following integral:
Here are a few examples: