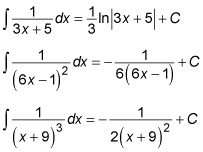Your first step in any problem that involves partial fractions is to recognize which case you’re dealing with so that you can solve the problem. The simplest case in which partial fractions are helpful is when the denominator is the product of distinct linear factors — that is, linear factors that are nonrepeating.
For example, you can change this:
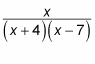
to this:
Keep in mind that for each distinct linear factor in the denominator, you need to add a partial fraction of the following form:
For example, suppose that you want to integrate the following rational expression:
The denominator is the product of three distinct linear factors — x, (x + 2), and (x – 5) — so it’s equal to the sum of three fractions with these factors as denominators:
The number of distinct linear factors in the denominator of the original expression determines the number of partial fractions. In this example, the presence of three factors in the denominator of the original expression yields three partial fractions.
You have two ways to find the unknowns in a sum of partial fractions. The easy and quick way is by using the roots of polynomials. Unfortunately, this method doesn’t always find all the unknowns in a problem, though it often finds a few of them. The second way is to set up a system of equations.
When a sum of partial fractions has distinct linear factors, you can use the roots of these linear factors to find the values of unknowns:
To find the values of the unknowns A, B, and C, first get a common denominator on the right side of this equation (the same denominator that’s on the left side):
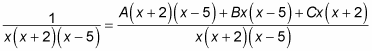
Now multiply both sides by this denominator:
1 = A(x + 2)(x – 5) + Bx(x – 5) + Cx(x + 2)
To find the values of A, B, and C, substitute the roots of the three factors (0, –2, and 5):

Plugging these values back into the original equation gives you:
This expression is equivalent to what you started with, but it’s much easier to integrate. To do so, use the Sum Rule to break it into three integrals, the Constant Multiple Rule to move fractional coefficients outside each integral, and variable substitution to do the integration. Here’s the answer so you can try it out:
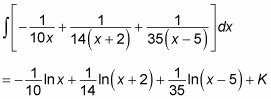
This answer uses K rather than C to represent the constant of integration to avoid confusion, because you already used C in the earlier partial fractions.
When you start out with a distinct linear factor, using partial fractions leaves you with an integral in the following form:
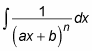
Integrate by using the variable substitution u = ax + b so that du = a dx and
This substitution results in the following integral:
Here are a few examples: