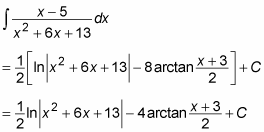For example, suppose that you want to integrate this function:
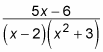
The first factor in the denominator is linear, but the second is quadratic and can’t be decomposed to linear factors. So set up your partial fractions as follows:
The number of distinct quadratic factors in the denominator tells you how many partial fractions you get. So in this example, two factors in the denominator yield two partial fractions.
Working systematically with a system of equations
Setting up a system of equations is an alternative method for finding the value of unknowns when you’re working with partial fractions. It’s not as simple as plugging in the roots of factors, but it’s your only option when the root of a quadratic factor is imaginary.Here’s a problem to illustrate this method:
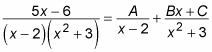
To start out, see how far you can get by plugging in the roots of equations. Begin by getting a common denominator on the right side of the equation:
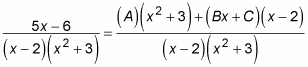
Now multiply the whole equation by the denominator:
5x – 6 = (A)(x2 + 3) + (Bx + C)(x – 2)
The root of x – 2 is 2, so let x = 2 and see what you get:
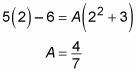
Now you can substitute
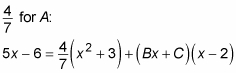
Unfortunately, x2 + 3 has no root in the real numbers, so you need a different approach. First, get rid of the parentheses on the right side of the equation:
Next, combine similar terms (using x as the variable by which you judge similarity). This is just algebra:
Because this equation works for all values of x, you now take what appears to be a questionable step, breaking this equation into three separate equations as follows:
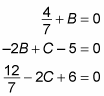
At this point, a little algebra tells you that
So you can substitute the values of A, B, and C back into the partial fractions:
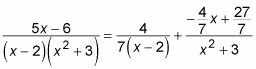
You can simplify the second fraction a bit:
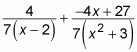
Quadratic factors of the form (ax2 + C)
When you start out with a quadratic factor of the form (ax2 + C), using partial fractions results in the following two integrals: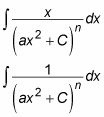
Integrate the first by using the variable substitution u = ax2 + C so that du = 2ax dx and
This substitution results in the following integral:
Here are some examples:
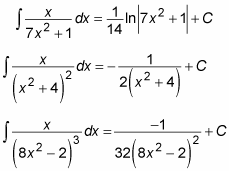
To evaluate the second integral, use the following formula:
Quadratic factors of the form (ax2 + bx + C)
Most math teachers have at least a shred of mercy in their hearts, so they don’t tend to give you problems that include this most difficult case. When you start out with a quadratic factor of the form (ax2 + bx + C), using partial fractions results in the following integral: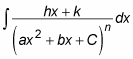
Okay, that’s way too many letters and not nearly enough numbers. Here’s an example:
This is about the hairiest integral you’re ever going to see at the far end of a partial fraction. To evaluate it, you want to use the variable substitution u = x2 + 6x + 13 so that du = (2x + 6) dx. If the numerator were 2x + 6, you’d be in great shape. So you need to tweak the numerator a bit. First multiply it by 2 and divide the whole integral by 2:
Because you multiplied the entire integral by 1, no net change has occurred. Now add 6 and –6 to the numerator:
You have added 0 to the integral, which didn’t change its value. At this point, you can split the integral in two:
At this point, you can use variable substitution to change the first integral as follows:
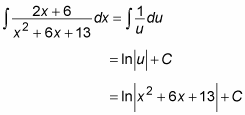
To solve the second integral, complete the square in the denominator: Divide the b term (6) by 2 and square it, and then represent the C term (13) as the sum of this and whatever’s left:
Now split the denominator into two squares:
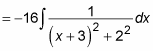
To evaluate this integral, use formula shown in the previous section:
So here’s the final answer for the second integral:
Therefore, piece together the complete answer as follows: