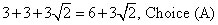You’ll find lots of triangles on the PSAT/NMSQT, especially right triangles. The Greeks weren’t the only mathematicians in the ancient world, but they managed to place their “brand” on geometry, a word which, by the way, comes from the Greek words for “earth measure.” Specifically, a mathematician named Pythagoras wrote the Pythagorean Theorem:
a2 + b2 = c2
You can use this formula to find the sides of any right triangle, in which a and b are defined as the two legs of the triangle and c is the hypotenuse, a fancy word for the side opposite the 90̊ angle. Note: This formula — the Pythagorean Theorem — appears in the information box on the exam.
A few common right-triangle ratios are frequent fliers on the PSAT/NMSQT, so it’s worth memorizing them:
The 3:4:5 triangle: The sides can be any multiple of these numbers (for example, 15:20:25, with each side multiplied by 5, or 21:28:35, with each side multiplied by 7).
The 5:12:13 triangle: Strange numbers, huh? But this ratio behaves like any other, so you can multiply each side by 2 and get a 10:24:26 triangle, or multiply by 5 and get a 25:60:65 triangle.
The
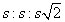
triangle: The s stands for a side, and because you have two sides that are equal (both are s), this is an isosceles right triangle, and the interior angles are 45°, 45°, and 90°. Note: This formula appears in the information box on the exam.
You can use the information in the preceding bullet to calculate the diagonal (a line connecting opposite corners) of a square. If the sides of a square are 65 meters long, the diagonal is
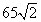
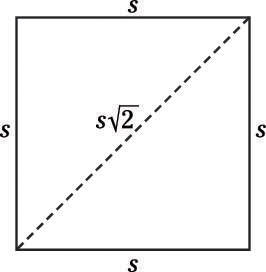
You can easily see why this formula works: A square is just two isosceles right triangles glued together, because each side of a square is the same length.
The
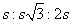
triangle: This one has 30°-60°-90° angles, and for some reason, the exam-writers love it. The hypotenuse (the long side) is double the length of the side opposite the 30º angle. Note: This formula appears in the information box on the exam.
If you cut an equilateral triangle (one with equal sides) in half, you get two 30°-60°-90° triangles. So if you see a question on the exam about an equilateral triangle, drag out this formula and you’ll find the answer in a flash.
Stretch those triangular muscles! Try these problems:
An equilateral triangle has a side with a length of x. What is the area of the triangle, in terms of x?
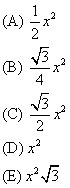
What is the area of the following figure?
(A) 6
(B) 15
(C) 32
(D) 36
(E) 42
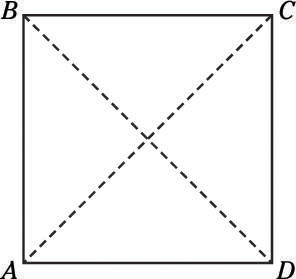
In the following square, the product of diagonals AC and BD is 18. What is the perimeter of triangle ABC?
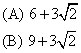
(C) 18
(D) 24
(E) 36
Now check your answers.
B.
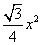
Always draw a picture if you’re having any trouble visualizing a problem:
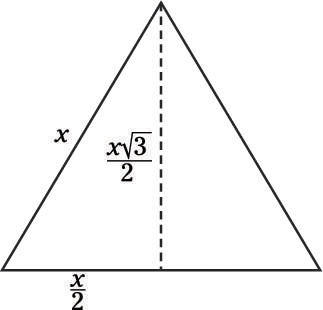
Remember that you can transform all equilateral triangles into a pair of 30º-60º-90º triangles by cutting them in half. That lets you see that the base of one of the smaller triangles is x/2, and the height is
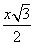
making the area of the whole triangle equal
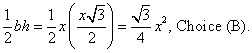
D. 36
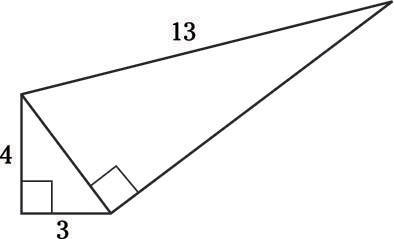
How well do you know your Pythagorean triples? Either way, you can use the Pythagorean Theorem to help you solve this problem, or any problem with right triangles. First, look at the small triangle. Its area is
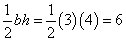
Next, you can quickly solve for the hypotenuse using a2 + b2 = c2, b = 12 and determine that it’s 5 units long.
Pythagorean theorem to the rescue again: 52 + b2 = 132, b = 12. That means that the area of the larger triangle is
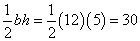
Add those two areas together: 6 + 30 = 36, and you can see that Choice (D) is correct.
A.
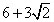
Diagonals AC and BD must be the same length, so they’re each
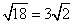
in length. Now you can ignore the square and just pay attention to triangle ABC, which is a 45̊-45̊-90̊ triangle, with a hypotenuse of
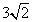
Using your knowledge of special triangles (or the formula box), you know that the legs of the triangle must each be 3 units long. Therefore, the perimeter of the triangle is