Say you’re filling up your swimming pool and you know how fast water is coming out of your hose, and you want to calculate how fast the water level in the pool is rising. You know one rate (how fast the water is being poured in), and you want to determine another rate (how fast the water level is rising). These rates are called related rates because one depends on the other — the faster the water is poured in, the faster the water level will rise. In a typical related rates problem, the rate or rates you’re given are unchanging, but the rate you have to figure out is changing with time. You have to determine this rate at one particular point in time.
For example, say you’re blowing up a balloon at a rate of 300 cubic inches per minute. When the balloon’s radius is 3 inches, how fast is the radius increasing?
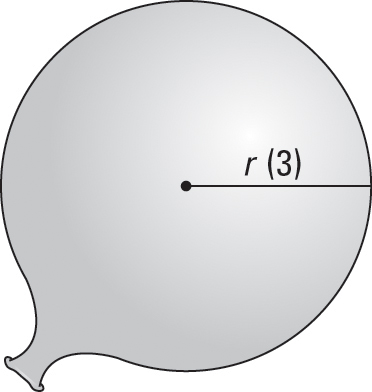
Draw a diagram labeling the diagram with any unchanging measurements (there aren’t any in this unusually simple problem) and make sure to assign a variable to anything in the problem that’s changing (unless, of course, it’s irrelevant to the problem).
The radius in the figure is labeled with the variable r. The radius needs a variable because, as the balloon is being blown up, the radius is changing. In the figure, 3 is in parentheses to emphasize that the number 3 is not an unchanging measurement. The problem asks you to determine something when the radius is 3 inches, but remember, the radius is constantly changing.
In related rates problems, it’s important to distinguish between what is changing and what is not changing.
The volume of the balloon is also changing, so you need a variable for volume, V. You could put a V on your diagram to indicate the changing volume, but there’s really no easy way to label part of the balloon with a V like you can show the radius with an r.
List all given rates and the rate you’re asked to determine as derivatives with respect to time.
You’re pumping up the balloon at 300 cubic inches per minute. That’s a rate — it’s a change in volume (cubic inches) per change in time (minutes). So,

You have to figure out how fast the radius is changing, so
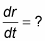
Write down the formula that connects the variables in the problem, V and r.
Here’s the formula for the volume of a sphere:
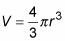
Differentiate your formula with respect to time, t.
This works like implicit differentiation because you’re differentiating with respect to t, but the formula is based on something else, namely r.
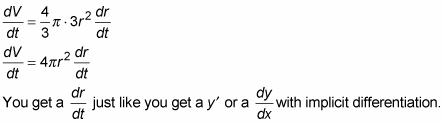
Substitute known values for the rate and variables in the equation from Step 4, and then solve for the thing you’re asked to determine.

Be sure to differentiate (Step 4) before you plug the given information into the unknowns (Step 5).

So, the radius is increasing at a rate of about 2.65 inches per minute when the radius measures 3 inches. Think of all the balloons you’ve blown up since your childhood. Now you finally have the answer to the question that’s been bugging you all these years.
By the way, if you plug 5 into r, rather than 3, you get an answer of about 0.95 inches per minute. This fact should agree with your balloon-blowing-up experience — the bigger the balloon gets, the slower it grows.

