Capacitors store energy for later use. The voltage and current of a capacitor are related. The relationship between a capacitor’s voltage and current define its capacitance and its power. To see how the current and voltage of a capacitor are related, you need to take the derivative of the capacitance equation q(t) = Cv(t), which is
Because dq(t)/dt is the current through the capacitor, you get the following i-v relationship:
This equation tells you that when the voltage doesn’t change across the capacitor, current doesn’t flow; to have current flow, the voltage must change. For a constant battery source, capacitors act as open circuits because there’s no current flow.
The voltage across a capacitor changes in a smooth fashion (and its derivatives are also smoothly changing functions), so there are no instantaneous jumps in voltages.
Just as you don’t have gaps in velocities when you accelerate or decelerate your car, you don’t have gaps in voltages. The mass of the car causes a smooth transition when going from 55 miles per hour to 60 miles per hour.
In a similar and analogous way, you can think of the capacitance C as the mass in the circuit world that causes a smooth transition when changing voltages from one value to another.
To express the voltage across the capacitor in terms of the current, you integrate the preceding equation as follows:
The second term in this equation is the initial voltage across the capacitor at time t = 0.
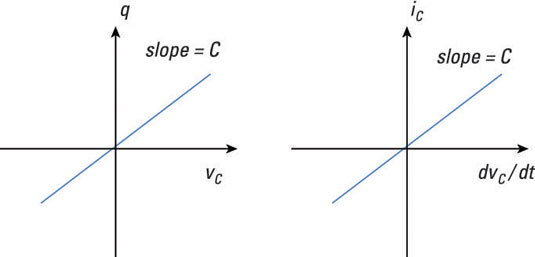
You can see the i-v characteristic in the graphs shown here. The left diagram defines a linear relationship between the charge q stored in the capacitor and the voltage v across the capacitor. The right diagram shows a current relationship between the current and the derivative of the voltage, dvC(t)/dt, across the capacitor with respect to time t.
Think of capacitance C as a proportionality constant, like a resistor acts as a constant in Ohm’s law.






