The idea of sampling from a population is one of the most fundamental concepts in statistics — indeed, in all of science. For example, you can't test how a chemotherapy drug will work in all people with lung cancer; you can study only a limited sample of lung cancer patients who are available to you and draw conclusions from that sample.
As used in clinical research, the terms population and sample can be defined this way:
Population: All individuals having a precisely defined set of characteristics (for example: human, male, age 18–65, with Stage 3 lung cancer)
Sample: A subset of a defined population, selected for experimental study
Any sample, no matter how carefully it is selected, is only an imperfect reflection of the population, due to the unavoidable occurrence of random sampling fluctuations. The figure, which shows IQ scores of a random sample of 100 subjects from the U.S. population, exhibits this characteristic. (IQ scores are standardized so that the average for the whole population is 100, with a standard deviation of 15.)
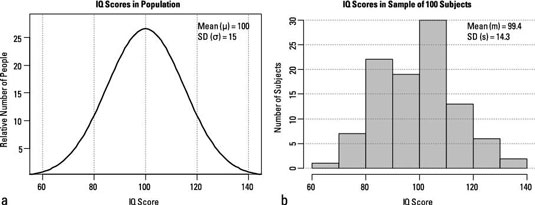
The sample is distributed more or less like the population, but clearly it's only an approximation to the true distribution. The mean and standard deviation of the sample are close to, but not exactly equal to, the mean and standard deviation of the population, and the histogram doesn't have a perfect bell shape. These characteristics are always true of any random sample.
Histograms are prepared from data you observe in your sample of subjects, and they describe how the values fluctuate in that sample. A histogram of an observed variable, prepared from a random sample of data, is an approximation to what the true population distribution of that variable looks like.
In an ideal experiment, sampling is carried out so that every member of the population has the same chance of being selected for the experimental sample. In such a random sample, only unavoidable random sampling fluctuations, of the kind illustrated in the figure above.
But in most real-life experiments, it's impossible to perform truly random sampling of the entire population. You can't try to recruit adult male stage 3 lung cancer patients from every part of the world, so your sample will almost certainly have a race distribution different from that in the global population. This produces what's called sampling bias. If your sample differs from the population with respect to some variable that can affect the outcome of your experiment, it can limit the applicability of your experiment's outcome to the population in general.






