A double integral allows you to measure the volume under a surface as bounded by a rectangle. Definite integrals provide a reliable way to measure the signed area between a function and the x-axis as bounded by any two values of x. Similarly, a double integral allows you to measure the signed volume between a function z = f(x, y) and the xy-plane as bounded by any two values of x and any two values of y.
Here’s an example of a double integral:
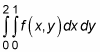
Although it may look complicated, a double integral is really an integral inside another integral. To help you see this, the inner integral in the previous example is bracketed off here:
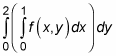
When you focus on the integral inside the brackets, you can see that the limits of integration for 0 and 1 correspond with the dx — that is, x = 0 and x = 1. Similarly, the limits of integration 0 and 2 correspond with the dy — that is, y = 0 and y = 2.
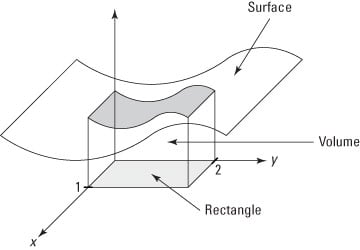
This figure shows you what this volume looks like. The double integral measures the volume between f(x, y) and the xy-plane as bounded by a rectangle. In this case, the rectangle is described by the four lines x = 0, x = 1, y = 0, and y = 2.

