In physics, to take angles (or direction) into account when measuring force, you need to do a little vector addition. Take a look at the following figure. Here, the mass m isn’t moving, and you’re applying a force F to hold it stationary. Here’s the question: What force is the pulley’s support exerting, and in which direction, to keep the pulley where it is?
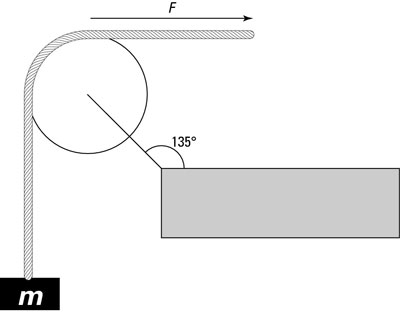
You’re sitting pretty here. Because the pulley isn’t moving, you know that
on the pulley. So what are the forces on the pulley? You can account for the force due to the mass’s weight, which has magnitude mg and is directed straight down. Putting that in terms of vector components, it looks like this (keep in mind that the y component of Fmass has to be negative, because it points downward, which is along the negative y-axis):
You also have to account for the force of the rope on the pulley, which, because you’re holding the mass stationary and the rope transmits the force you’re applying, must be of magnitude mg and directed to the right — along the positive x-axis. That force looks like this:
You can find the force exerted on the pulley by the rope and the mass by adding the vectors Fmass and Frope:
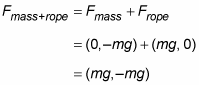
The force exerted by both the mass and the rope, Fmass + rope, is (mg, –mg).
You know that the total force on the pulley is zero (because it is not accelerating):
Two forces are acting on the pulley,
so the sum of these two must be zero:
This means that
Therefore, Fsupport must equal
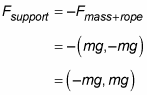
As you can see by checking the figure, the directions of this vector make sense — the pulley’s support must exert a force to the left (–mg) and upward (+mg) to hold the pulley where it is.
You can also convert Fsupport to magnitude and direction form, which gives you the full magnitude of the force. The magnitude is equal to
Note that this magnitude is greater than the force you exert or the force the mass exerts on the pulley because the pulley support has to change the direction of those forces.
Now find the direction of the force Fsupport. You can find the angle it makes with the horizontal axis, theta, using the components of the force. You know from basic trigonometry that the components can be expressed in terms of theta, like so:
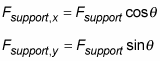
where Fsupport indicates the magnitude of the force in these equations. This relates the components of the vector to its magnitude and direction; you can use this to isolate the direction in terms of the components in the following way: If you divide the y component by the x component in the preceding form, you find the tangent of the angle:
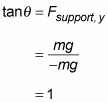
Now if you take the inverse tangent, you get an answer for theta:
However, this answer can’t be right, because this angle would mean that the force pointed to the right and up. But you may remember that angles that differ by a multiple of 180 degrees give the same tangent, so you can subtract the preceding answer from 180 degrees to get
This direction is to the left and upward and has the correct tangent, so this is the direction of the force. Checking with the figure above, we see that the direction of the force happens to be parallel to the support rod.
If you get confused about the signs when doing this kind of work, check your answers against the directions you know the force vectors actually go in. A picture’s worth a thousand words, even in physics!

