In physics, if a fluid is flowing at a certain speed at a certain point in a system of pipes, you can predict what its speed will be at another point by using the equation of continuity. Because the mass of the fluid is neither created nor destroyed, if mass moves away from one place at a certain rate, it must therefore move to the neighboring place at the same rate. With this idea expressed as an equation, you can find out how the speed changes in a narrowing pipe, for example.
The equation of continuity comes from the idea that no mass disappears when fluid is flowing. In other words, the fluid you get out equals what you put in. You can find the equation of continuity by mixing a little geometry with the physics formulas for mass (which remains constant), density, and speed.
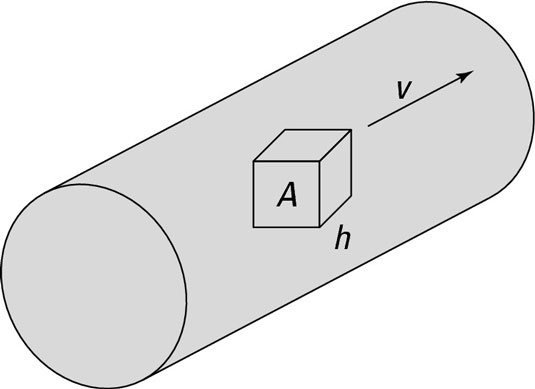
Imagine a cube of fluid flowing in a pipe with the rest of the fluid, as the figure shows. The cube has an area A perpendicular to the fluid flow and has a length h along the fluid flow.
Now say that the pipe narrows so much that the cube no longer fits. The boundary of the cube is going to change shape. What can you say stays constant between the original cube and the deformed cube? The mass of the fluid inside the box shape will stay constant because no fluid flows through the boundary. Therefore, you can say that
m1 = m2
where m1 is the mass of the fluid in the first cube and m2 is the mass of the fluid in the deformed cube later on, where the pipe narrows.
If you instead look at the situation in terms of density,
the mass of the fluid in the cube is the density multiplied by the volume of the cube, which is Ah. So you can restate the equation as
where A1 is the area of the front face of the cube originally, h1 is the original length of the cube, and so on.
Now say you’re measuring the amount of mass going by in time t to get the flow rate, so you divide the equation you just got by a time interval, t:
The length of the cube passing you by in time t gives you the speed of the fluid at that location, so h/t becomes the speed of the fluid at that location. Substituting v, the speed, for h/t, you get the following equation:
And this quantity,
is called the mass flow rate — it’s the mass of fluid that passes by a certain point per second. The MKS (meter-kilogram-second) units of the mass flow rate are kilograms per second, or kg/s.
The mass flow rate has the same value at every point in a fluid conduit that has a single entry and single exit point. The mass flow rate at any two points along the conduit can be related like this, with the equation of continuity:






