The business world is characterized by numerous decisions made over an extended period of time. In managerial economics, game theory helps to figure out the best decision to make. A payoff is associated with each decision, and the players also have memory of past decisions. For all practical purposes, the business time horizon is infinite — the game is never-ending. The result is an infinitely repeated game.
In infinitely repeated games, you need to take into account not only how your rival plays this round, but also how this round of the game influences future rounds.
Another factor you must consider in infinitely repeated games is the time value of money. A dollar received today is worth more than a dollar received one year from now, because the dollar received today can earn interest. Thus, future payoffs must be adjusted by using the present value calculation.
The typical strategy used in an infinitely repeated game is the trigger strategy. A trigger strategy is contingent on past play — a player takes the same action until another player takes an action that triggers a change in the first player’s action.
An example of a trigger strategy used in games involving a prisoner’s dilemma is tit-for-tat. When you use a tit-for-tat strategy, you start by assuming players cooperate. In any subsequent round, you do whatever your rival did in the previous round. Thus, if your rival cheated on an understanding in the last round, you cheat this round. If your rival cooperated in the last round, you cooperate this round.
A tit-for-tat strategy tends to lead to cooperation because it punishes cheaters in the next round. In addition, it forgives cheaters if they subsequently decide to cooperate. One requirement of the tit-for-tat strategy is that the players are stable. The players remember how the game was played in the previous period. New players can upset the necessary balance by not having the required memory of past behavior.
In this example, there are two railroads you may recognize from the board game Monopoly — the Pennsylvania Railroad and the B & O Railroad. Here, they’re competing for traffic between the same cities. The railroads can either cheat on one another and charge low prices for freight, or they can cooperate and charge high prices. The illustration shows the resulting payoff table of annual profits.
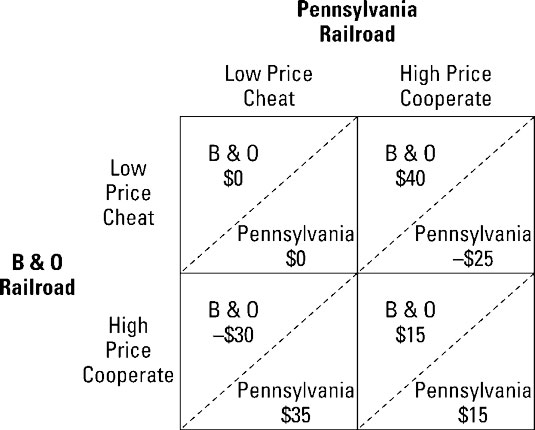
In this payoff table, both railroads have a dominant action — to charge a low price. As a result, they both earn $0. This result is yet another prisoner’s dilemma.
If these railroads play the game a long time, they both recognize that cooperating by charging a high price allows both to earn $15 million each and every year. Cheating by charging a low price may lead to a large payoff one year, but the cost associated with having your rival cheat in the next year is very high. Consider what happens in a tit-for-tat strategy:
If the B & O Railroad charges a high price, and the Pennsylvania Railroad cheats and charges a low price, B & O’s losses are $30 million and Pennsylvania’s profit is $35 million.
Following a tit-for-tat strategy, the B & O Railroad charges a low price the next year, and the Pennsylvania Railroad continues to charge a low price.
The railroads are locked into a situation of zero profit forever, because the B & O Railroad continues to charge the low price that the Pennsylvania Railroad charged the previous year. The railroads are in a prisoner’s dilemma.
Following a tit-for-tat strategy, the B & O charges a low price the next year and the Pennsylvania Railroad charges a high price.
The B & O Railroad earns $40 million in profit and Pennsylvania loses $25 million. But now the game can return to cooperation. The B & O forgives the Pennsylvania Railroad for cheating in the first round and in future rounds, each railroad earns $15 million.
In some sense, the Pennsylvania Railroad has to accept punishment for cheating in the first place. But accepting that punishment one year leads to a situation where both railroads return to $15 million annual profit. If the railroads continue to cheat by charging a low price, each will recognize that cooperation does not pay, and they will be forever locked into charging a low price and receiving zero profit.
In this infinite game, both railroads make more profit if they cooperate the entire time and never fall into a tit-for-tat strategy.
If you have an infinite time horizon, the present value of a constant stream of future net revenue equals
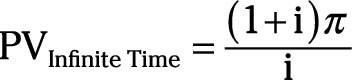
where ð is the net revenue earned each year and i is the interest rate.
In the previous example, if the B & O and Pennsylvania railroads cooperate, they each earn $15 million annual profit. If the B & O Railroad has an infinite time horizon, the present value of $15 million annual profit at a 5 percent interest rate is
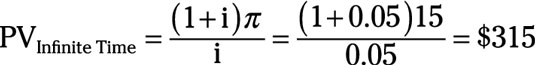
or $315 million.






