In physics, when the temperature remains constant as other quantities change, you have what is called an isothermal system. The remarkable apparatus in the first figure shows an example of an isothermal system.
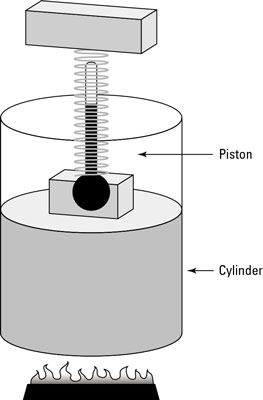
It’s specially designed to keep the temperature of the enclosed gas constant, even as the piston rises. When you apply heat to this system, the piston rises or lowers slowly in such a way as to keep the product of pressure times volume constant. Because PV = nRT, the temperature stays constant as well. (Remember that n is the number of moles of gas that remains constant, and R is the gas constant.)
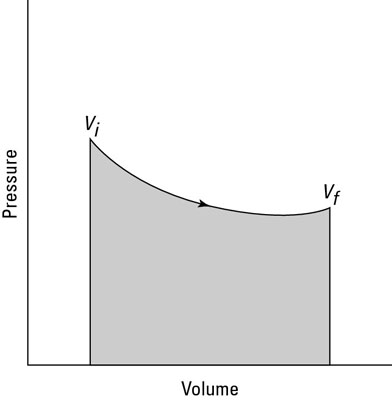
What does the work look like as the volume changes? Because PV = nRT, the relation between P and V is
You can see this equation graphed in the second figure, which shows the work done as the shaded area underneath the curve. But what the heck is that area?
The work done in an isothermal process is given by the following equation, where ln is the natural log (ln on your calculator), R is the gas constant
Vf is the final volume, and Vi is the initial volume:
Because the temperature stays constant in an isothermal process and because the internal energy for an ideal gas equals (3/2)nRT, the internal energy doesn’t change. Therefore, you find that heat equals the work done by the system:
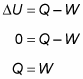
If you immerse the cylinder you see in the first figure in a heat bath, what would happen? The heat, Q, would flow into the apparatus, and because the temperature of the gas stays constant, all that heat would become work done by the system.
Say that you have a mole of helium to play around with on a rainy day of temperature 20 degrees Celsius, and for fun you decide to expand it from Vi = 0.010 m3 to Vf = 0.020 m3. What’s the work done by the gas in the expansion? All you have to do is plug in the numbers:

The gas does 1,690 joules of work. The gas’s change in internal energy is 0 joules, as always in an isothermal process. And because Q = W, the heat added to the gas is also equal to 1,690 joules.
Here’s another example. Say that you’re given 2.0 moles of hydrogen gas at a temperature of 600 kelvins for your birthday. Expanding the gas from a volume of 0.05 cubic meters to 0.10 meters isothermally, you wonder how much work the gas does, so you get out your clipboard. The work done by an ideal gas during isothermal expansion is
Plugging in the numbers and doing the math gives you
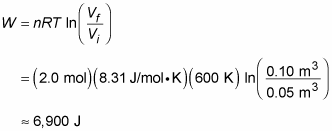
So the gas does 6,900 joules of work during its expansion.
So what about the change in the internal energy of the gas? You know that the change in internal energy is

the isothermal expansion.






