Here are some examples:
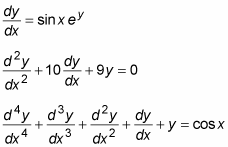
Solving a differential equation means finding the value of the dependent variable in terms of the independent variable. The following examples use y as the dependent variable, so the goal in each problem is to solve for y in terms of x.
An ordinary differential equation (ODE) has only derivatives of one variable — that is, it has no partial derivatives. Here are a few examples of ODEs:
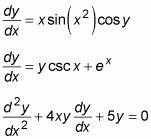
In contrast, a partial differential equation (PDE) has at least one partial derivative. Here are a few examples of PDEs:
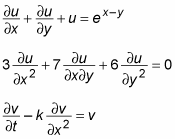
DEs are further classified according to their order. This classification is similar to the classification of polynomial equations by degree.
First-order ODEs contain only first derivatives. For example:
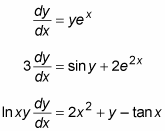
Higher-order ODEs are classified, as polynomials are, by the greatest order of their derivatives. Here are examples of second-, third-, and fourth-order ODEs:

As with polynomials, generally speaking, a higher-order DE is more difficult to solve than one of lower order.
What constitutes a linear differential equation depends slightly on who you ask. For practical purposes, a linear first-order DE fits into the following form:
where a(x) and b(x) are functions of x. Here are a few examples of linear first-order DEs:
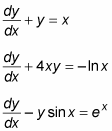
Linear DEs can often be solved, or at least simplified, using an integrating factor.
A linear second-degree DE fits into the following form:
where a, b, and c are all constants. Here are some examples:
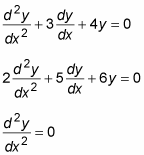
Note that the constant a can always be reduced to 1, resulting in adjustments to the other two coefficients.

