Share This
How to Write Prime Factorization of Composite Numbers
Prime factorization shows you the only way a number can be factored. The process of prime factorization breaks down a composite number into the prime numbers that, when multiplied together, give you that composite number. Every number’s prime factorization is unique.
(The opposite of prime numbers, composite numbers, can be broken down into factorable, reducible pieces. Whole numbers larger than 1 that aren’t prime are composite numbers.)
A good way of writing out prime factorizations is to do an upside-down division:
You put a prime factor on the outside left and the result or quotient (the number of times it divides evenly) underneath.
You divide the quotient (the number underneath) by another prime number and keep doing this until the bottom number is a prime.
Then you can stop. The order you do this in doesn’t matter. You get the same result or list of prime factors no matter what order you use.
Before you go, take a look at the prime factorization of 120:
5
Use the numbers from the left to write out the prime factorization.
Look at the numbers going down the left side of the work and the number at the bottom. They act the same as the divisors in a division problem. Only, in this case, they’re all prime numbers. Although many composite numbers could have played the role of divisor for the number 120, the numbers for the prime factorization of 120 must be prime-number divisors.
When using this process, you usually do all the 2s first, all the 3s, then all the 5s, and so on to make the prime factorization process easier, but you can do this in any order:
120 = 2 × 2 × 2 × 3 × 5 = 23 × 3 × 5
Here are some examples of how to write out the prime factorizations of composite numbers:
6 = 2 × 3
12 = 2 × 2 × 3 = 22 × 3
16 = 2 × 2 × 2 × 2 = 24
250 = 2 × 5 × 5 × 5 = 2 × 53
510,510 = 2 × 3 × 5 × 7 × 11 × 13 × 17
42,059 = 137 × 307
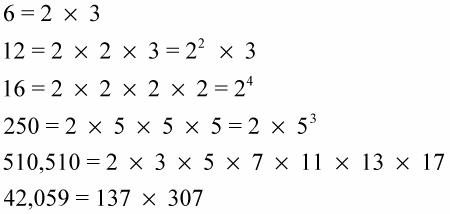
The factors of some numbers aren’t always obvious. Finding the prime factorization of numbers like the last example above without a calculator, computer, or list of primes is difficult.
Algebra GlossaryThe letter (pi) from the Greek alphabet refers to the ratio of the circumference of a circle to its diameter, which is approximately 3.14 or 22/7.
Algebra GlossaryAn operation that tells you how far a number is from zero.
Algebra GlossaryNumber with the same numerical part but the opposite sign (plus or minus) of the given number. If zero is the sum of two numbers, then these two numbers are additive inverses of one another.
Algebra GlossaryMeasure of a specified region in a plane.
Algebra GlossaryCharacteristic of addition and multiplication that allows the grouping of terms to change without affecting the result.
Algebra GlossaryValue multiplied repeatedly in an exponential expression.
Algebra GlossaryProcess requiring two values to produce a third value.
Algebra GlossaryTwo terms separated by addition or subtraction.
Algebra GlossaryGrouping symbol that looks like this: { }.
Algebra GlossaryGrouping symbol that looks like this: [ ].
Algebra GlossaryDistance around the outside of a circle.
Algebra Glossary1. A number that multiplies a variable and tells how many of the variable. 2. The number preceding a variable.
Algebra GlossaryMethod of counting that tells how many ways a designated number of objects can be selected from a given set.
Algebra GlossarySame value on the bottom of more than one fraction.
Algebra GlossaryCharacteristic of addition and multiplication that allows the order of the values in an operation to be changed without affecting the result.
Algebra GlossaryWhole number larger than 1 that isn’t prime.
Algebra GlossaryVariable or number that never changes in value in an expression.
Algebra GlossaryPart of an ordered pair that designates a point’s location on a coordinate plane.
Algebra GlossaryFlat region determined by two intersecting, perpendicular, numbered lines called axes.
Algebra Glossary1. The third power of a number. 2. The result of multiplying a number by itself three times.
Algebra GlossaryNumber that you can multiply by itself three times to get a given number. For example, the cube root of eight is two because two multiplied by itself three times equals eight.
Algebra GlossaryAdjective that describes an expression in which the highest power is three.
Algebra GlossaryFraction with an unwritten denominator of 10 indicated by the decimal point
Algebra GlossaryNumber of degrees between 1 and 360 that comprise the measure of an angle.
Algebra GlossaryHighest power occurring in the expression.
Algebra GlossaryBottom number of a fraction.
Algebra GlossaryLongest distance across a circle.
Algebra GlossaryResult of subtraction.
Algebra GlossaryNumerals from zero through nine, so called because they were originally counted on the fingers.
Algebra GlossaryCharacteristic of multiplication and addition that allows for the multiplication of each individual term in a grouped series by a term outside of the grouping without changing the value of the expression.
Algebra GlossaryA number to be divided by another number.
Algebra GlossaryOne number can be divided by another with no remainder.
Algebra GlossarySolution that appears twice when solving an equation because the related factor appears twice in the factored form. For example, in (y – 2)(y – 2) = 0, y = 2 is a double root or solution. In (y – 2)(y – 2)(x + 3) = 0, y = 2 is still a double root or solution.
Algebra GlossaryMathematical statement with an equal sign showing that two values are equal.
Algebra GlossaryFractions equal to one another, even though they may have different denominators. (Example: 3/4 and 75/100)
Algebra GlossaryA number that can be divided or is divisible by 2.
Algebra GlossaryValue in smaller type found above and to the right of the base that indicates the number of times the base is multiplied by itself.
Algebra GlossaryCombination of values (variables, numbers, and/or constants) and operation(s).
Algebra Glossary1. (noun) Any of the values involved in a multiplication problem that when multiplied together produces a result. 2. (verb) To rewrite an algebraic expression as a product.
Algebra GlossaryOperation that multiplies a whole number by every counting number smaller than it.
Algebra Glossary1. Acronym for first, outer, inner, and last — which indicates the order in which two terms (one from each of two binomials) are multiplied together. 2. The process of multiplying two binomials.
Algebra GlossaryRule or method that is accepted as true and used over and over in common applications.
Algebra GlossaryAny quantity expressed as a numerator (the value above the bar) and a denominator (the value below the bar).
Algebra GlossaryLine separating the numerator from the denominator.
Algebra GlossaryPlotted figure in a plane.
Algebra GlossaryLargest possible value that evenly divides each term of an expression containing two or more terms.
Algebra GlossaryParentheses, brackets, and braces that can affect the order of operations. Terms and operations within the grouping symbol take precedence.
Algebra GlossaryTerms and operations within grouping symbols.
Algebra GlossaryLongest side of right triangle.
Algebra GlossaryA fraction whose numerator is larger than the denominator.
Algebra GlossaryRelationship between two unequal values.
Algebra GlossaryWithout end; uncountable, as in a repeating decimal
Algebra GlossaryA positive or negative whole number or zero; numbers starting with zero and going up or down in increments of one.
Algebra GlossaryPoint where a graph crosses the x-axis or y-axis.
Algebra GlossaryPoint shared by two lines.
Algebra GlossaryNumber with no fractional equivalent whose decimal never repeats or terminates.
Algebra GlossaryAll the points in the coordinate plane that satisfy a linear equation.
Algebra GlossaryAdjective describing expression or equation in which the highest power of any variable is one. Constants can be higher powers. For example, x + y = 4 is linear.
Algebra GlossaryStatus of a fraction whose numerator and denominator cannot be divided evenly by the same number. A fraction with a numerator of 12 and a denominator of 25 is in lowest terms.
Algebra GlossaryImproper fraction written as a whole number alongside a fraction.
Algebra GlossaryAn expression with only one term.
Algebra GlossaryA number evenly divisible by a specific factor. Example, 14 and 21 are multiples of 7.
Algebra GlossaryRule stating if the product of two numbers is zero, then one of the numbers must be zero.
Algebra GlossaryAn integer multiplied with both the numerator and denominator of a fraction.
Algebra GlossaryValues starting with 1 and increasing by 1.
Algebra GlossaryAny quantity that is less than zero; usually preceded by a minus sign.
Algebra GlossaryTwo numbers, one positive and one negative, whose product is negative one.
Algebra GlossaryWhen two or more grouping symbols are inside one another, such as {32[4 × 2(2 + 5)]}.
Algebra GlossaryA set of numbers.
Algebra GlossaryThe top number in a fraction.
Algebra GlossaryA whole number that is not evenly divided by 2.
Algebra GlossaryMathematical process, such as addition, subtraction, multiplication, and division, performed on one or more quantities.
Algebra GlossaryTwo values inside parentheses and separated by a comma that indicate the position of a point in the coordinate plane.
Algebra GlossaryPoint of intersection of the x-axis and y-axis in a coordinate plane.
Algebra GlossaryLines that never intersect and are always the same distance apart.
Algebra GlossaryFractions with a denominator of 100. The percentage is the numerator of the fraction — how many out of 100.
Algebra GlossaryTotal distance around the outside of a region or area.
Algebra GlossaryCounting method that determines the number of ordered arrangements there are when a certain number of objects are selected from a given set.
Algebra GlossaryLines that form a 90-degree angle at their intersection.
Algebra GlossaryThe letter (π) from the Greek alphabet refers to the ratio of the circumference of a circle to its diameter, which is approximately 3.14 or 22/7.
Algebra GlossaryExpression with one or more terms.
Algebra GlossaryAny quantity greater than zero.
Algebra GlossaryAny number raised to the power of zero equals 1 as long as the base number isn’t zero.
Algebra GlossaryA prime number that evenly divides the number you’re working on.
Algebra GlossaryProcess of finding the prime numbers that, when multiplied together, produce a given composite number.
Algebra GlossaryWhole number larger than the number 1 that can be divided evenly only by itself and 1.
Algebra GlossaryPositive number that when multiplied by itself produces a given positive number. For example, the square roots of 25 are 5 and −5, but the principal square root of 25 is only 5.
Algebra GlossaryThe result of multiplication.
Algebra GlossaryFraction whose value is less than 1. The numerator is always smaller than the denominator.
Algebra GlossaryEquation showing that two ratios are equal to one another.
Algebra GlossaryFormula specific to right triangles stating that the hypotenuse (c) squared is equal to the sum of the squares of the remaining sides (a and b): a2 + b2 = c2.
Algebra GlossaryOne of four regions in a coordinate plane defined by the x-axis and the y-axis.
Algebra GlossaryAlso known as second degree, expression or equation in which the highest power is 2. The degree is 2.
Algebra GlossaryResult of division.
Algebra GlossarySymbol for the operation to find a square root.
Algebra GlossaryDistance from the center of a circle to its outer edge; half its diameter.
Algebra GlossaryMultiplying a base number the number of times indicated by the exponent. For example, 5 is being raised to the power of 3 in expression 53.
Algebra GlossaryQuantity, positive or negative, that can be written as a fraction; its decimal equivalent terminates or repeats.
Algebra GlossaryAny rational or irrational number.
Algebra Glossary1. Two numbers whose product is always 1, such as 3 × 1/3 and 0.25 × 4. 2. Either one of the two numbers in a reciprocal. Example: 3 is the reciprocal of 1/3; and 1/3 is the reciprocal of 3.
Algebra GlossaryFour-sided plane figure with all right angles; its opposite sides are equal to one another in length.
Algebra GlossaryProcess in which a common factor of the numerator and denominator of a fraction is divided out, leaving an equivalent fraction.
Algebra GlossaryTwo numbers that have no factors in common other than the number 1.
Algebra GlossaryValue that is left over when one number is divided by another.
Algebra GlossaryA decimal in which beyond a certain point a digit or set of digits repeats indefinitely. (Example: 3.3333… and 3.1787878…) Rounding off results in an estimated or approximate value.
Algebra Glossary90-degree angle.
Algebra GlossaryThree-sided plane figure with a 90-degree angle (right angle).
Algebra GlossaryValue that multiplied by itself a number of times results in the value or number wanted, such as 2 is the root of 4, because 2 multiplied by itself produces 4.
Algebra GlossaryApproximating the value to the nearest digit or decimal place, such as rounding 14.9 up to 15.
Algebra GlossaryA standard way of writing very large and very small numbers as the product of two values — a number between 1 and 19 and a power of 10. Scientific notation follows the form N × 10a where N is a number from 1 up to 10, but not 10 itself, and a is an integer (positive or negative number).
Algebra GlossaryHalf the perimeter.
Algebra GlossarySymbol indicating whether a value is positive (+) or negative (−).
Algebra GlossaryA fraction in which both the numerator and the denominator are whole numbers.
Algebra GlossaryTo combine all that can be combined and put an expression in its most easily understandable form.
Algebra GlossaryNumber indicating the measure of a line’s steepness or slant and whether it rises or falls.
Algebra GlossaryValue(s) of the variable that make the equation a true statement.
Algebra GlossaryFind the answer or what number the variable stands for.
Algebra Glossary1. Product of another number times itself. 2. Value with an exponent of 2.
Algebra GlossaryValue resulting in a given value when multiplied by itself. For example, the square root of 4 is 2, because 2 ×2 = 4, which is a perfect square.
Algebra GlossaryMethod of replacing a value with its equivalent.
Algebra GlossaryResult of addition.
Algebra GlossaryCharacteristic of equations that allows for the exchange of the value(s) on one side of the equal sign with the value(s) on the other side (quantities on the right go to the left; quantities on the left go to the right) without changing the truth of the equation: If x = y, then y = x.
Algebra GlossaryShort-cut division process in which only the coefficients of the terms in an expression are used. The answer is obtained by multiplying and adding.
Algebra GlossaryGroup of number(s) and/or variable(s) connected to one another by multiplication or division and separated from other terms by addition or subtraction.
Algebra GlossaryExpression with three terms. Each term is separated from the others by addition or subtraction.
Algebra GlossaryTo factor a trinomial into two binomials
Algebra GlossaryA numeric equivalence or worth of an expression or variable.
Algebra GlossaryLetter representing an unknown number or what you’re solving for in an algebra problem.
Algebra GlossaryCorner of a figure; where two sides intersect to form an angle.
Algebra GlossaryMeasurement of the amount of space within a three-dimensional solid figure.
Algebra GlossaryAll natural numbers plus zero. Start with zero and add one repeatedly to find the whole number spectrum (0, 1, 2, 3 . . . ).
Comments (1)
Leave a Reply