Sometimes, finding a measure isn't so easy. You may have to deal with an irregular shape, like a triangle, or even calculate your way around a fixed object. Whatever the case, you can use trigonometry to find the answers you've been searching for.
The most commonly used formula for the area of a triangle is
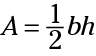
where A is the area, b is the length of the triangle's base, and h is the height of the triangle drawn perpendicular to that base.
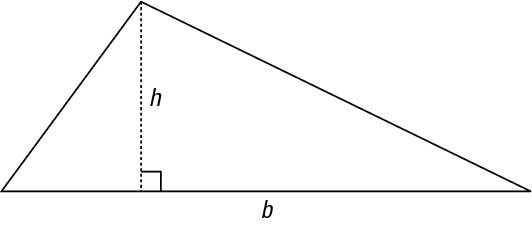
This area formula works fine if you can get the measure of the base and the height, and if you can be sure that you've measured a height that's perpendicular to the side of the triangle. But what if you have a triangular yard — a big triangular yard — and have no way of measuring some perpendicular segment to one of the sides?
One alternative is to use Heron's Formula, which uses the measures of all three sides. The other alternative, of course, is to use trigonometry — or, at least, a formula with an angle measure in it.
To measure that angle, you can be very sophisticated and get a surveying apparatus, or if you've got a protractor handy, you can do a decent estimate by extending the sides at an angle for a bit and eyeballing the angle size.
The trig formula for finding the area of a triangle is
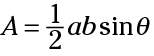
where a and b are two sides of the triangle and theta is the angle formed between those two sides. You don't need the measure of the third side at all, and you certainly don't need a perpendicular side.
Take a look at the triangle shown, with sides a and b and the angle between them.
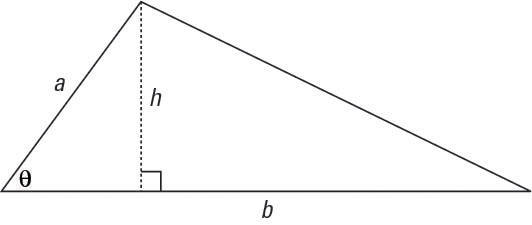
Start with the traditional formula for the area of this triangle,
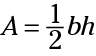
Then look at the smaller triangle to the left. (Because the height is drawn perpendicular to the base, the sides and height form a right triangle.) The acute angle theta has a sine equivalent to the following:
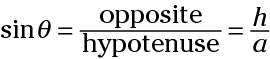
If you solve that equation for h by multiplying each side by a, you get
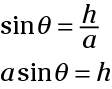
Replace the h in the traditional formula with its equivalent from the preceding equation, and you get

Check out how this formula works in an actual problem. The triangle shows the measures of two of its sides and the angle between them.
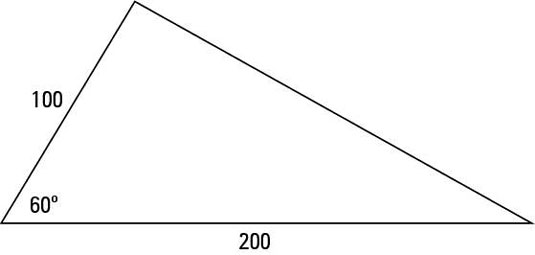
To find the area of the triangle:
Use the formula

inserting the values that you know.

Solve for the value of the area.

The area is about 8,660 square units.





