Before reading this article, you should check out the discussion of trig substitution in the companion article, “How to Use Trig Substitution to Integrate.”
With the trigonometric substitution method, you can do integrals containing radicals of the following forms:
This article concerns the first form which you tackle with the sine function. The other two forms are handled with the tangent and secant functions and are discussed in other articles.
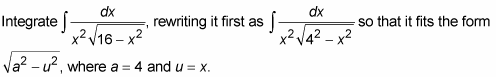
Draw a right triangle where

You should confirm this with the Pythagorean theorem.

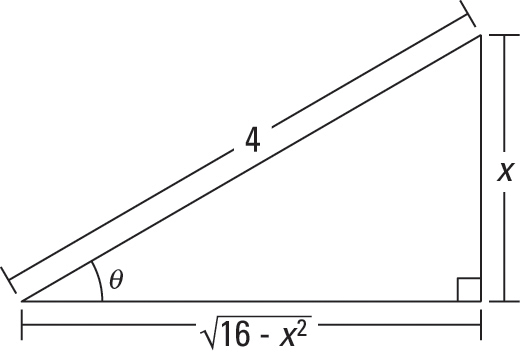
the following figure shows a SohCahToa triangle.
Solve

then differentiate, and solve for dx.

Find which trig function equals the radical over the a (that’s the a from

not a as in adjacent), and then solve for the radical.
Look at the triangle in the figure.

Use the results from Steps 2 and 3 to make substitutions in the original problem and then integrate.

The triangle shows that

So substitute back for your final answer:

It’s a walk in the park.






