The shell method allows you to measure the volume of a solid by measuring the volume of many concentric surfaces of the volume, called “shells.” Although the shell method works only for solids with circular cross sections, it’s ideal for solids of revolution around the y-axis, because you don’t have to use inverses of functions.
Here’s how it works:
Find an expression that represents the area of a random shell of the solid in terms of x.
Use this expression to build a definite integral (in terms of dx) that represents the volume of the solid.
Evaluate this integral.
You can use a can of soup — or any other can that has a paper label on it — as a handy visual aid to give you insight into how the shell method works. To start out, go to the pantry and get a can of soup.
Suppose that your can of soup is industrial size, with a radius of 3 inches and a height of 8 inches. You can use the formula for a cylinder to figure out its volume as follows:
V = Ab · h = 32π · 8 = 72π
You can also use the shell method, shown here.
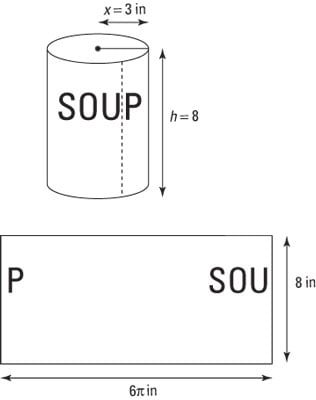
To understand the shell method, slice the can’s paper label vertically, and carefully remove it from the can, as shown in the figure. (While you’re at it, take a moment to read the label so that you’re not left with “mystery soup.”)
Notice that the label is simply a rectangle. Its shorter side is equal in length to the height of the can (8 inches) and its longer side is equal to the circumference (2π · 3 inches = 6π inches). So the area of this rectangle is 48π square inches.
Now here’s the crucial step: Imagine that the entire can is made up of infinitely many labels wrapped concentrically around each other, all the way to its core. The area of each of these rectangles is:
A = 2π x · 8 = 16π x
The variable x in this case is any possible radius, from 0 (the radius of the circle at the very center of the can) to 3 (the radius of the circle at the outer edge). Here’s how you use the shell method, step by step, to find the volume of the can:
Find an expression that represents the area of a random shell of the can (in terms of x):
A = 2π x · 8 = 16π x
Use this expression to build a definite integral (in terms of dx) that represents the volume of the can.
Remember that with the shell method, you’re adding up all the shells from the center (where the radius is 0) to the outer edge (where the radius is 3). So use these numbers as the limits of integration:
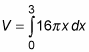
Evaluate this integral:
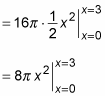
Now evaluate this expression:
= 8π (3)2 – 0 = 72π
The shell method verifies that the volume of the can is 72π cubic inches.

