Quantum physicists understand that matter exhibits wave-like properties, which means that matter, like waves, aren't localized in space. This fact inspired Werner Heisenberg, in 1927, to come up with his celebrated uncertainty principle.
You can completely describe objects in classical physics by their momentum and position, both of which you can measure exactly. In other words, classical physics is completely deterministic.
On the atomic level, however, quantum physics paints a different picture. Here, the Heisenberg uncertainty principle says that there's an inherent uncertainty in the relation between position and momentum. In the x direction, for example, it looks like this:
where
is the measurement uncertainty in the particle's x position,
is the measurement uncertainty in its momentum in the x direction and
That is to say, the more accurately you know the position of a particle, the less accurately you know the momentum, and vice versa. This relation holds for all three dimensions:
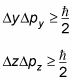
And the Heisenberg uncertainty principle is a direct consequence of the wave-like nature of matter, because you can't completely pin down a wave.
Quantum physics, unlike classical physics, is completely nondeterministic. You can never know the precise position and momentum of a particle at any one time. You can give only probabilities for these linked measurements.

