You’ll be surprised how much headway you can often make when you integrate an unfamiliar trigonometry function by first tweaking it using the Basic Five trig identities:
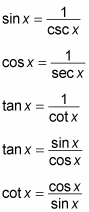
The unseen power of these identities lies in the fact that they allow you to express any combination of trig functions into a combination of sines and cosines. Generally speaking, the trick is to simplify an unfamiliar trig function and turn it into something that you know how to integrate.
When you’re faced with an unfamiliar product or quotient of trig functions, follow these steps:
Use trig identities to turn all factors into sines and cosines.
Cancel factors wherever possible.
If necessary, use trig identities to eliminate all fractions.
For example:
In its current form, you can’t integrate this expression. So you follow these steps to turn it into an expression you can integrate:
Use the identities

Cancel both sin x and cos x in the numerator and denominator:

In this example, even without Step 3, you have a function that you can integrate.
= –cos x + C
Here’s another example:
Again, this integral looks like a dead end before you apply the five basic trig identities to it:
Turn all three factors into sines and cosines:
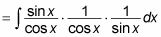
Cancel sin x in the numerator and denominator:

Use the identity cos x = 1/sec x to eliminate the fraction:

This turns an unfamiliar function into a trig function that you know how to integrate.






