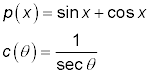How to Use Function Notation

Function notation is like shorthand writing: if you understand it, you’ll save a lot of time (and pencil lead) when working out a problem. Without notation, defining a function or explaining how it works can involve a lot of words and can get rather lengthy and awkward.

Imagine having to write, “Square the input, multiply that result by 2, and then subtract 3.” Mathematicians are an efficient lot, and they prefer a more precise, quick way of writing their instructions. Function notation is just that.

First, functions are generally named with letters — the most frequently used is the oh-so-obvious f. (Mathematicians may be efficient, but they’re not necessarily original or creative.) If you want the function f to be the rule for squaring a number, multiplying that result by 2, and then subtracting 3, you would write the function as

You read the function like this: “F of x is equal to two times x squared minus 3.” The x is a variable — in this case, the input variable. Whatever you put in the parentheses after the f replaces any x in the rule. Just use the order of operations to perform any computations. In the first equation that follows, an 8 replaces the x. In the second equation, a –4 replaces the x. Each time, the function produces only one answer:

Don’t feel bound to the f, though. You can use other letters to name the functions and the input variables. Sometimes you use letters that represent what’s going on or what you’re using the formula for, such as finding area, interest, or cost:

And, of course, you have the trig functions. Some trig functions involving sine, cosine, and secant are