This is the toughest part of solving math word problems on the ASVAB. The hardest thing about doing word problems is taking the English words and translating them into mathematics. Luckily, math word problems often contain certain keywords that can help.
Addition keywords
Several words and phrases used in math word problems indicate an addition operation:
Increased by
More than
Combined
Together
Total of
Sum
Added to
“The drill sergeant can do 100 pushups more than Private Jones” is equivalent to Private Jones + 100 = drill sergeant. “Together, they can do 300 pushups” can be mathematically stated as drill sergeant + Private Jones = 300.
Try the following example, just to see if you’re getting the hang of things:
The drill sergeant can do 100 pushups more than Private Jones. Together, they can do 300 pushups. How many pushups can Private Jones do?
The question is asking you how many pushups Private Jones can do. You’re not really interested in how many the drill sergeant can do, and the problem statement tells you that they can do 300 total pushups together. You also know that the drill sergeant can do 100 more than Private Jones.
List the important information:
Let j = the number of pushups that Private Jones can do. This figure is what you really want to find out, so you need to define it first.
Let d = the number of pushups that the drill sergeant can do. This is a necessary fact in order to solve the problem.
You know another definition of d. The problem statement tells you that the drill sergeant can do 100 more pushups than Private Jones, which means that d = j + 100, which is the same (mathematically) as saying j = d – 100.
You know that together they can do 300 pushups, which tells you that d + j = 300.
All you need to do now is to solve that final equation in terms of j. First, subtract d from both sides to express the equation in terms of j: d + j = 300 is the same as j = 300 – d.
You already have a definition for d from above (d = j + 100). Substitute this value for d in the equation you’re now working to solve:
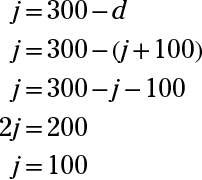
Private Jones can do 100 pushups.
Because math can be a tricky thing, it’s a good idea to check your answer to make sure it makes sense. Plug your answer into the original problem and see whether it works out: The drill sergeant can do 100 pushups more than Private Jones: 100 + 100 = 200. The drill sergeant can do 200 pushups. Together, they can do 300 pushups: 100 + 200 = 300.
Subtraction keywords
If you see any of the following words and phrases in a math word problem, it generally indicates a subtraction operation:
Decreased by
Minus
Less
Difference between/of
Less than
Fewer than
“Becky’s pay decreased by $10” can be stated mathematically as Becky – 10. This phrasing is also the same as “Becky’s pay minus $10,” or “Becky’s pay less $10.”
“The difference between Bob’s pay and Becky’s pay” can be expressed as Bob – Becky.
The less than and fewer than terms work backward in English from what they are in the math. Although “Becky’s pay minus $10” is Becky – 10, “Becky’s pay less than x” is not Becky – x; it’s x – Becky.
Multiplication keywords
The following words and phrases usually mean a mathematical multiplication operation when included in a math word problem:
Of
Times
Multiplied by
Product of
Increased/decreased by a factor of
“15 percent of x” is mathematically expressed as x · 0.15. “x times y” and “x multiplied by y” mean x · y. The product of x and y is the same as x · y.
Increased by a factor of and decreased by a factor of can involve addition and subtraction in combination with multiplication. “x increased by a factor of 10 percent” is expressed as x + (x · 0.10).
Division keywords
If you see the following words/phrases in a math word problem, “division operation” should pop into your mind:
A
Per
Average
Ratio of
Quotient of
The first two terms in this list mean “divided by” — for example, “I bought 2 gallons of milk at the grocery store and paid $3, so milk was $1.50 a gallon,” or “Milk was $1.50 per gallon.”
To find the average of a group of numbers, you add the numbers, and then divide by the number of terms. “The average of a, b, and c” is (a + b + c) ÷ 3.
Mathematically, ratios are expressed as fractions. A ratio of five to three is written as
The “quotient of x and y” is the same as x ÷ y.
Practicing keywords
Learning how to recognize keywords is essential in translating English into mathematical expressions. Try a few examples, just to see if you’re getting the hang of it:
Translate “the sum of 13 and y” into an equation. This phrase translates to 13 + y. The keyword sum indicates an addition operation.
How do you write “the quotient of a and 6” as an equation? The keyword quotient means division, so this example translates to a ÷ 6.
Are you ready to try a longer one?
The length of a rectangle is 45 inches more than its width. Let the width = w; express the length in mathematical terms. More than is a keyword that means addition. Because the width = w, you write the length mathematically as w + 45.






