How to Translate a Function's Graph

Moving a function's graph horizontally or vertically is called a translation. In other words, you translate every point on the parent graph left, right, up, or down. The kinds of translations fall into two categories — horizontal shifts and vertical shifts.

Horizontal shifts

A number adding or subtracting inside the parentheses (or other grouping device) of a function creates a horizontal shift. Such functions are written in the form f (x – h), where h represents the horizontal shift.

The numbers in this function do the opposite of what they look like they should do. For example, if you have the equation

Why does it work this way? Examine the parent function

The g (x) function acts like the f (x) function when x was 0. In other words, f (0) = g (3). It’s also true that f (1) = g (4). Each point on the parent function gets moved to the right by three units; hence, three is the horizontal shift for g (x).

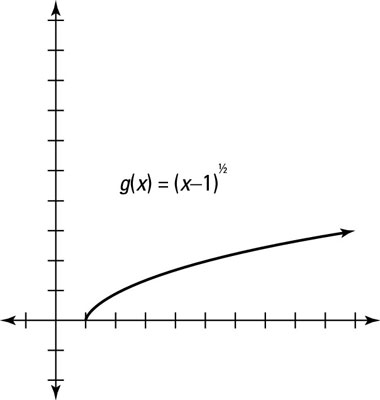
Because – 1 is underneath the square root sign, this is a horizontal shift — the graph gets moved to the right one position.

(the parent function), you’ll find that k (0) = g (1), which is to the right by one. The above figure shows the graph of g (x).

Vertical shifts

Adding or subtracting numbers completely separate from the function causes a vertical shift in the graph of the function. Consider the expression f (x) + v, where v represents the vertical shift. Notice that the addition of the variable exists outside the function.

Vertical shifts are less complicated than horizontal shifts because reading them tells you exactly what to do. In the equation

you can probably guess what the graph is going to do — it moves down four units. The graph of

moves up three.

You see no vertical stretch or shrink for either f (x) or g (x) because the coefficient in front of x-squared for both functions is 1. If another number multiplied with the functions, you’d have a vertical stretch or shrink.

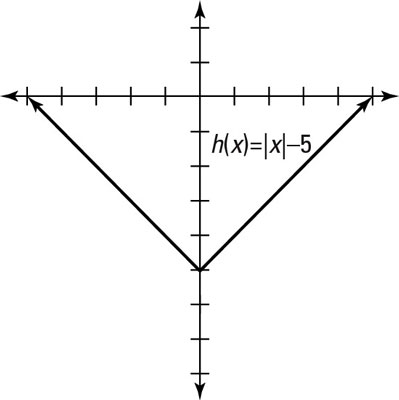
To graph the function h (x) = |x| – 5, notice that the vertical shift is down five units. The above figure shows this translated graph.