When you work on both sides of a trig identity at the same time, you may sometimes need to square both sides. You generally use this technique when one side or the other (or both) has a radical. This method is also good to use when you’re solving some types of trig equations. Squaring both sides has benefits twofold: It gets rid of radicals, and it creates terms that can be part of one of the Pythagorean identities. The Pythagorean identities have wonderful substitutions.
This first example has only one radical, and it’s on the right side. Solve the identity
![]()
-
Square both sides of the identity.
Be sure to expand the squared binomial on the left correctly.

-
Rearrange the terms in the numerator.

-
Replace 1 + cot2x with its equivalent by using the Pythagorean identity.
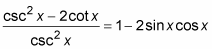
-
Split up the fraction by writing each term in the numerator over the denominator.

-
Simplify the first term. Rewrite the numerator and denominator in the second term by using the ratio and reciprocal identities.

-
Simplify the complex fraction by flipping the denominator and multiplying it by the numerator.







