When solving trigonometry equations, more than one method will usually work — although one method is often quicker or easier than another. With practice, you’ll get good at choosing the better of the ways to solve the equation.
And then you’ll come across a trig equation that defies your finest attempts. Two methods that you can use when solving these more difficult trig equations are: to square both sides of the equation, or to multiply each term through by a trig function that you’ve carefully selected.
Examples of equations that respond well to squaring both sides include
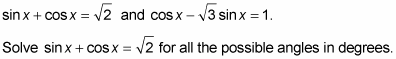
Square both sides of the equation.
When squaring a binomial, be sure not to forget the middle term.
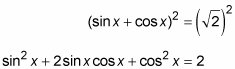
Use the Pythagorean identity to replace sin2 x + cos2 x.
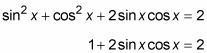
Subtract 1 from each side. Then replace the expression on the left with the sine double-angle formula.
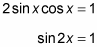
Solve for the value of 2x by using the inverse function. Then write a few angle solutions to determine a pattern.
2x = sin–1(1) = 90°, 450°, 810°, . . .
Because you’re supposed to find all the possible solutions, you’re not bound by only two rotations.
Divide every term by 2.
2x = 90°, 450°, 810°, . . .
x = 45°, 225°, 405°, . . .
Write an expression for all the solutions.
x = 45° + 180°n
In the next example, you need to do a little shifting at first.
equation by itself. Otherwise, when you square both sides, you end up with a radical factor in one of the terms. That situation isn’t always bad, but dealing with it is usually a little more awkward than not.
Solve the equation for all the possible angles from 0 to 360 degrees.
Add the radical term to both sides and subtract 1 from both sides.
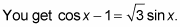
Square both sides.
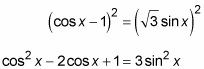
Replace sin2 x with 1 – cos2 x from the Pythagorean identity.
Doing so creates an equation with terms that have all the same functions, cos x, in them.
cos2 x – 2cos x + 1 = 3(1 – cos2 x)
Simplify the equation by distributing the 3 on the right and then bringing all the terms to the left to set the equation equal to 0.
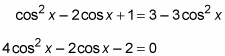
Divide every term by 2.
2cos2 x – cos x – 1 = 0
Factor the quadratic equation.
(2cos x + 1)(cos x – 1) = 0
Set each factor equal to 0.
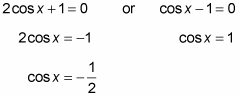
Solve each equation for the value of x.
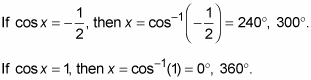
The angles 0 and 360 degrees have the same terminal side. You usually list just one of them: 0 degrees.

