When two lines meet they form an angle. Angles are measured in degrees. On the PSAT/NMSQT, you won’t find any negative or zero angles, and you probably won’t have to deal with fractional angles either (no 45.9°, for example). You do have to know these basic facts:
-
A right angle measures 90°. Right angles are a very big deal because they show up in a lot of formulas. If you see one, pay attention.
-
The sum of angles around a point is 360°. Think of the lines forming a circle around a center point. Note: This fact appears in the information box on the exam.
-
A straight-line angle equals 180°. When two lines meet head-on, they create a straight-line angle, which just sits there looking like a straight line. If a line cuts through a straight line, the two angles formed are supplementary or supplemental, math terms that mean the two angles add up to 180°.
-
Angles opposite each other are equal. These angles are also called vertical angles. In this diagram, x and y are vertical angles.
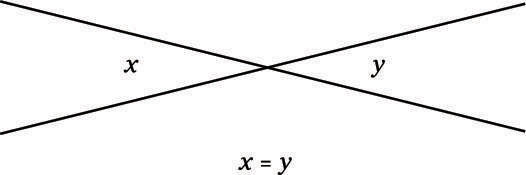
You may see the phrase vertical angles in a test question. Don’t assume that vertical angles are standing up just because in other contexts vertical means upright. Vertical angles are opposite each other, regardless of whether they’re up and down or side by side.
-
If a line cuts through parallel lines, the small angles at one intersection measure the same as the small angles at the other intersection. Similarly, the big angles at one intersection equal the big angles at the other intersection. Take a look at this sketch:
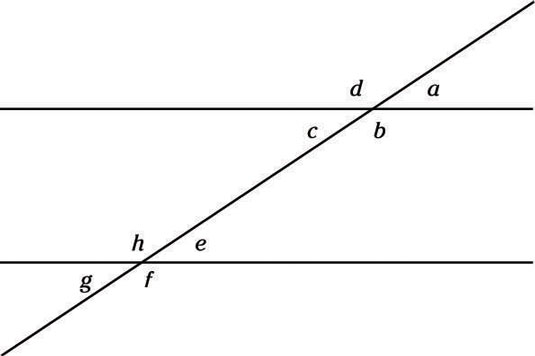
The small angles at the first intersection are a and c, and the small angles at the second intersection are e and g. All these angles are equal. So are the bigger angles: b and d and f and h. By the way, equal angles are called congruent in math-speak.
You won’t be quizzed on this information, but you may have to use it in a problem. Take a look at this question:
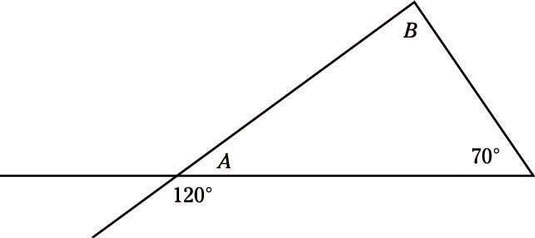
Suppose you’re asked to find B. A straight line equals 180°, so you can find A by subtracting 120° from 180°, which gives you 60°. You also know that the three angles of a triangle add up to 180°, so 60° + 70° + B = 180°. Therefore, B = 50°.
Your turn. Try these problems:
-
In the following figure, lines l and m are parallel. Determine the value of x.
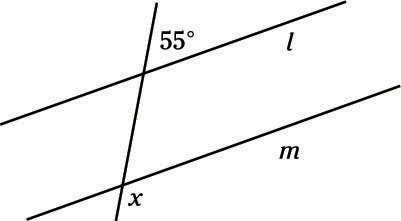
(A) 55°
(B) 75°
(C) 95°
(D) 125°
(E) 155°
-
Determine the measure of angle a.
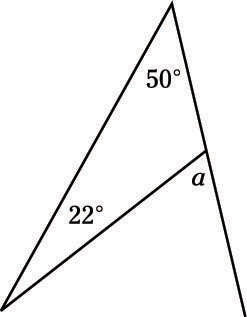
(A) 22°
(B) 33°
(C) 50°
(D) 72°
(E) 108°
-
Find the value of x in the following figure.
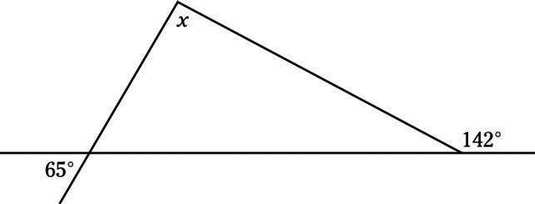
(A) 65°
(B) 77°
(C) 90°
(D) 103°
(E) 142°
Now check your answers.
-
D. 125°
Remember that lines cutting parallel lines form a whole bunch of equal angles. The small angles that the cut forms are all equal (in this problem, each is 55°), and all the large angles are also equal (in this problem, they equal x).
You can see that the 55° angle is supplementary to a large angle, so the two angles must add up to 180°. Subtract: 180° – 55° = 125°, so all the large angles, including x, must measure 125°, Choice (D).
-
D. 72°
You know that there are 180° in a triangle, so you can find the third angle in the triangle using subtraction: 180° – 50° – 22° = 108°. Now that you know that, you can see that 108° is supplemental to a, so a = 180° – 108° = 72°, or Choice (D).
-
B. 77°
Yet again, the key to this problem is knowing that there are 180° in a triangle. You know that the angle on the bottom left of the triangle measures 65° because it’s a vertical angle with the angle labeled 65°. You know that the angle on the bottom right of the triangle measures 38° because it’s supplementary to the 142° angle that’s labeled.
To find x, simply subtract those numbers from 180°: 180° – 65° – 38° = 77°, Choice (B).

