Age problems on the ASVAB involve figuring out how old someone is, was, or will be. You generally do solve them by comparing their ages to the ages of other people.
Sometimes you can solve an age problem by using a one-variable solution, and sometimes it takes several variables. As you will see, there are ways to solve the same problem by using either a one-variable solution or a two-variable solution.
One-variable solution
Sid is twice as old as Mary. In three years, the sum of their ages will be 66. How old are they now?
Let Mary’s age = x. Because Sid is twice as old as Mary, his age can be represented as 2x.
In three years, Mary’s age will be x + 3, and Sid’s age will be 2x + 3. The sum of their ages will be 66.
You now have an equation you can work with:
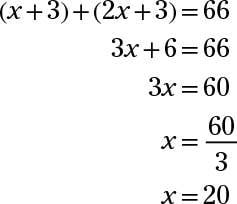
What did x stand for again? Was it Mary’s age or Sid’s age? Be sure to clearly label variables on your scratch paper, so you don’t get frustrated and tear your hair out in front of everyone else. That causes talk.
x represents Mary’s age, so Mary is 20 years old. Because Sid is twice Mary’s age, Sid is 40 (2 × 20 = 40).
If you have time, check your answer to see that it makes sense: Sid (age 40) is twice as old as Mary (age 20). In three years, the sum of their ages will be (40 + 3) + (20 + 3) = 43 + 23 = 66. It fits! Isn’t math fun?
Two-variable solution
Sid is twice as old as Mary. In three years, the sum of their ages will be 66. How old are they now?
Let m = Mary’s age and s = Sid’s age. You know that Sid is twice as old as Mary, so s = 2m. That gives you your first equation.
You also know that in three years, the sum of their ages will be 66. Stated mathematically:
(m + 3) + (s + 3) = 66
You can simplify this equation:
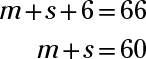
You now have two equations, with two variables that you can use to solve the problem:
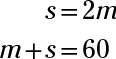
Replace s in the second equation with the definition of s in the first equation:
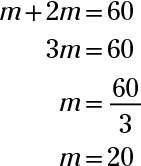
Mary is 20 years old. That’s the same answer you get when you use the one-variable solution.

